Bonjour,
Le lemme de Gauss nous affirme que si P est un polynôme à coefficients entiers factorisable dans
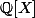
(i.e P=AB avec A et B des polynômes à coefficients rationnels), alors il existe
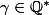
tel que
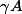
et
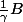
sont des polynômes à coefficients entiers (et donc P est factorisable dans
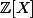
).
Ma question est la suivante :
Si P, A et B sont unitaires, peut-on affirmer que
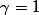
?
Pour plus de précision, dans la preuve du lemme de Gauss, la constante

est définie comme
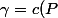\frac{\alpha A}{c(\alpha A)} =\frac{c(\beta B)}{\beta B})
où

et

sont des entiers telles que
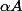
et
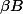
sont à coefficients entiers, et où

désigne le contenu d'un polynôme à coefficient entier (c'est-à-dire le pgcd de ses coefficients).
Merci d'avance pour votre aide,
Rhaegar
