Lemme de Cesàro - Suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 14 Fév 2014, 19:18
xNiicO a écrit:Est-ce grave si on s'arrête à N0 ? et pas N0 - 1.
Il y a pas de différence ? A mon avis ça revient quasiment au même.
Oui, c'est totalement kif-kif.
Et en fait, je me suis gourré : pour le 2em morceaux, si on va de No à n (inclus), ça ne fait pas n-No termes, mais plutôt n-No+1 ce qui est plus long à écrire que n-No donc c'est plutôt mieux d'aller de No+1 à n...
xNiicO a écrit:Sinon ça me parait clair, mais si on trouve à 3 epsilon prés, il faut partir au début sur :
Oui, on peut, mais je préfère faire constater une bonne fois pour toute que, si à la fin des calculs on obtient non pas epsilon "pile poil", mais une quantité qui tend vers 0 lorsque epsilon tend vers 0, ben ça marche aussi (et ça évite de "couper les epsilons en rondelles"...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 14 Fév 2014, 19:24
xNiicO a écrit:Mais je pense avoir compris quand même, ce que je trouve dans la méthode avec epsilon c'est que j'ai l'impression de tourner en rond et de rien prouver, si vous auriez un petit lien d'explication sur la méthode ça serait pas de refus.
L'explication "en clair", c'est que dans ta somme, lorsque n est "archi gigantesque", tu as des tas et des tas de termes qui sont proche de L et que les autres qui sont peu nombreux par rapport au gigantesque n que tu as pris, ben ils comptent pour du beurre à cause de la division par n.
Un peu plus détaillé comme explication, c'est mon post précédent...
Encore plus détaillé, c'est... la rédaction qu'il faut faire...
Essaye de le faire par toi même (ça restera mieux "ancré" que si tu ne fait que lire la rédaction d'un autre)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
xNiicO
- Membre Naturel
- Messages: 64
- Enregistré le: 18 Nov 2011, 22:23
-
par xNiicO » 14 Fév 2014, 19:30
Merci mais j'ai vu un peu comment tu raisonné :) Je vais le refaire et puis je questionnerais le prof en TD :)
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 15 Fév 2014, 19:40
Comme j'ai rien de mieux à faire, je te rédige la soluce :
On fixe un
.
Comme
, il existe un
(ne dépendant que de
) tel que :
.
Pour tout
on a alors
-L\right|\ <br />=\ \frac{1}{n}\left|\big(\sum_{k=1}^nU_k\big)-nL\right|\ <br />=\ \frac{1}{n} \left|\sum_{k=1}^n(U_k-L)\right|)
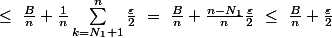
où
est une constante (i.e. une valeur ne dépendant que de
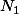
donc de
et ne dépendant pas de
) donc
à condition que
.
Conclusion : Si on prend
, on a
.
(et on revérifie bien que le
ne dépend
QUE de
et de rien d'autre.)
C.Q.F.D.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
xNiicO
- Membre Naturel
- Messages: 64
- Enregistré le: 18 Nov 2011, 22:23
-
par xNiicO » 19 Fév 2014, 12:00
Ben314 a écrit:Comme j'ai rien de mieux à faire, je te rédige la soluce :
On fixe un
.
Comme
, il existe un
(ne dépendant que de
) tel que :
.
Pour tout
on a alors
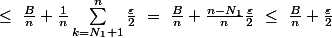
où
est une constante (i.e. une valeur ne dépendant que de
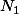
donc de
et ne dépendant pas de
) donc
à condition que
.
Conclusion : Si on prend
, on a
.
(et on revérifie bien que le
ne dépend
QUE de
et de rien d'autre.)
C.Q.F.D.
Super merci mais je comprends pas pourquoi tu pars de epsilon/2 alors qu'on pourrait garder epsilon normal non ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
par Sylviel » 19 Fév 2014, 12:21
Pour avoir epsilon à la fin. Ce n'est pas indispensable, mais pour être rigoureux et montrer la définition exacte c'est ce qu'il faut faire.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
