Lemme de borel-Cantelli

[arnaud26]

Bonjour je rappelle le lemme de Borel-Cantelli : Soit (X,T,u) un espace mesuré. Si les ensembles En sont tel que somme(u(En))< infini alors u(limsup(En))=0.
J'aimerais savoir si la réciproque est vraie c'est-à-dire savoir si pour tout ensemble E de mesure nulle, il existe une suite d'ensemble {En} tel que limsup(En)=E et tel que somme(u(En))
merci d'avance

[tize]

Bonjour,
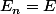
sans trop se fatiguer je dirais de prendre pour tout entier ...

[arnaud26]

effectivement j'ai oublié un certain détail qui empêche cette solution triviale la question aurait dû être :
j'aimerais savoir si pour tout ensemble E inclus dans R, de mesure nulle, il existe une suite d'intervalles {En} tel que limsup(En)=E et tel que somme(u(En))<infini. Et si tel est le cas, comment construire les intervalles En ?

[tize]

Bonsoir,
cela dépend de la mesure en question, si c'est une mesure régulière comme la mesure de Lebesgue alors pas de problème sinon ça me parait délicat...

[arnaud26]

On utilise la mesure de Lebesgue donc la mesure des intervalles En est en fait la longueur de ceux-ci.

[ThSQ]

effectivement j'ai oublié un certain détail qui empêche cette solution triviale la question aurait dû être :
j'aimerais savoir si pour tout ensemble E inclus dans R, de mesure nulle, il existe une suite d'intervalles {En} tel que limsup(En)=E et tel que somme(u(En))<infini. Et si tel est le cas, comment construire les intervalles En ?

Si on prend l'ensemble de Cantor : il est de mesure nulle, il ne contient aucun intervalle, il est indénombrable. J'ai du mal à imaginer une telle séquence de mais je manque peut-être d'imagination

[arnaud26]

mon but est en fait de trouver de tels intervalles pour l'ensemble

[ThSQ]

mon but est en fait de trouver de tels intervalles pour l'ensemble

Si tu admets les intervalles [a;a] c'est clair que c'est possible sinon je vois pas comment avec une limsup (une liminf oui).

[arnaud26]

non je ne peux utiliser des points comme intervalles car idéalement il me faudrait des intervalles ouverts !

[tize]

Bonjour,
uniquement avec des intervalles ce sera impossible comme te l'a dit ThSQ, par contre avec des ouverts (qui sont dans R union d'intervalles ouverts) c'est tout à fait possible...
La mesure de Lebesgue est extérieurement régulière donc pour mesurable tel que et pour tout il existe un ouvert tel que . De là on peut construire pour tout entier non nul un ouvert tel que et ...on a bien