je dois démontrer l'innégalité suivante. Mais je ne sais pas trop comment l'ataquer... Si quelqu'un peut me donner quelques pistes SVP. Merci d'avance
Leibniz pour le laplacian
2 messages
- Page 1 sur 1
Leibniz pour le laplacian
par Irrot » 30 Mar 2017, 07:41
Hello,
je dois démontrer l'innégalité suivante. Mais je ne sais pas trop comment l'ataquer... Si quelqu'un peut me donner quelques pistes SVP. Merci d'avance
 = ( \Delta f ) \,g + 2 \cdot( \nabla f ) \cdot ( \nabla g ) + f( \Delta g ))
je dois démontrer l'innégalité suivante. Mais je ne sais pas trop comment l'ataquer... Si quelqu'un peut me donner quelques pistes SVP. Merci d'avance
Re: Leibniz pour le laplacian
par capitaine nuggets » 30 Mar 2017, 08:23
Salut !
Rappelle-toi de la définition du laplacien :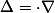
(produit scalaire de l'opérateur \nabla avec lui-même). Que vaut )
en fonction de 
, 
, 
et 
? Déduis-en alors  = \nabla \cdot (\nabla (fg))=...)
Rappelle-toi de la définition du laplacien :
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :