LCI (Groupe)

[pianozik]

S'ils vous plaît, j'arrive pas à trouver l'astuce, aidez moi si vous la voyez
L'enoncé:
Soit un groupe, l'élément neutre de dans , et deux éléments de vérifiant les relations suivantes :
; et
1) Soit H={ , }
Montrer que H est un sous-groupe de G
___________________________________________________________
Pour , on trouve que
Pour le symétrique, comme il est unique quand la loi est associative, , or cette forme n'est pas celle de l'ensemble H !!!!!!
Si quelqu'un a une idée je le remercie, Merci en avance

[tize]

Bonjour,
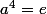
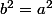
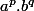
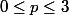
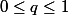
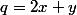
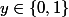
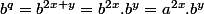
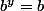
avec les hypothèses et il suffit alors d'envisager les produits avec et puisque si avec alors avec ou

[EDIT]
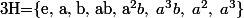
J'ajouterai qu'alors et c'est tout

[pianozik]

effectivement, mais c'est à démontrer pour la question suivante, donc je peux pas m'en servir mnt

[pianozik]

personne n'a une idée ?!

[tize]

Très sincèrement une autre méthode sans utiliser l'idée que je t'ai proposée, je ne vois pas...? A moins que a et b commutent mais je n'en suis vraiment pas sûr du tout...(ça m'étonnerai même beaucoup...)
Bon courage

[pianozik]

lol, je te remercie quand même
j'ai déjà tenté les cas de q pair ou impair, ça simplifie l'écriture, et quand je cherche le symétrique, je trouve qu'il a une forme différente de celle de H (surement il faut la modifier mais c'est ça qui veut pas se faire !!!!)

[Imod]

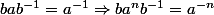
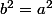
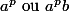
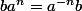
Une petite idée pour tout n . Comme les éléments de H sont de la forme . Comme , l'inverse de tout élément de H est dans H .

Imod

[pianozik]

H dépend de deux variables, p et q, les élements de H sont de cette forme
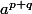
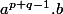
si est pair et si est impair

[Imod]

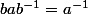
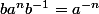
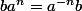
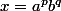
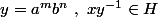
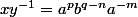
Pour détailler un peu , de la relation on déduit que pour tout entier n donc . Pour montrer que H est un groupe il suffit de montrer que pour tout et pour tout or et comme pour tout entier s , :
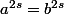
si q-n est pair :
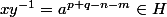
si q-n impair :

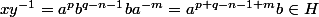
Donc H est un groupe .

Imod