Langage prédicat

[Cystravinsky]

Bonjour,

Existe-t-il s'il vous plaît une différence entre ces deux notations ?

Quelque soit λi appartenant à R, somme de i à n des λi

et

Quelque soit (λi,...,λn) appartenant à R^n, somme de i à n des λi

Merci par avance, bien à vous

Cystravinsky

[GaBuZoMeu]

Bonjour,

Déjà, les deux formules sont mal formées puisqu'on quantifie un terme et non une formule. Mais mettons que l'on a des points suspension pour donner une formule après le terme "somme des ".
La première formulation est incorrecte puisqu'on a un qui se promène on ne sait pas où. Il serait mieux de dire "Quel que soit pour 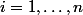" ou encore "Quel que soit , ..., quel que soit .
Ce n'est pas la même chose que la deuxième formule, mais ça veut dire la même chose.

[Cystravinsky]

Merci pour votre réponse GaBuZoMeu

En fait, ces deux écritures m'ont rendu confus dans ces deux définitions ci-dessous avec le quantificateur "il existe".

Si S= est une base de l'espace vectoriel E alors :



et Soit E un espace vectoriel et S= une famille d'éléments de E. Le sous-espace vectoriel engendré par S est :



On retrouve cette différence d'écriture avec le quantificateur "il existe", mais j'ai l'impression que c'est la même chose.

Quelle est s'il vous plaît la différence entre et hormis l'existence unique dans l'un et sachant qu'on a la même formule ensuite ?

Merci !

[Cystravinsky]

J'en suis arrivé à la conclusion que ces notations sont équivalentes :









La première sous-entendant que la variable muette i parcourt les entiers de 1 à n car nous avons la formule d'une somme qui l'explicite de suite après.

La dernière sous-entend que nous voulons bien un n-uplets même s'il n'y a pas de parenthèses.

Si quelqu'un trouve une erreur, merci de m'en informer !

Bien à vous

[GaBuZoMeu]

La première est franchement pas correcte.

[Cystravinsky]

C'est l'écriture de la première qui m'a fait douter sur le sens de toutes.

Je l'ai trouvée dans un livre d'algèbre pour prépa :

Soit E un espace vectoriel et un ensemble d'éléments de E.

Le sous-espace vectoriel engendré par S est :

[GaBuZoMeu]

Je suppose que tu as oublié de recopier le .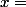
C'est incorrect parce que, comme je l'ai dit on ne sait pas ce que vient faire le dans le quantificateur. Dans l'écriture de la combinaison linéaire , le est une variable muette, cette somme est la même chose que . Bon, on comprend le sens, mais il n'empêche que c'est incorrect.

[Cystravinsky]

Oui en effet j'avais oublié le x=, je viens de le rajouter.

Merci pour les éclaircissements, je n'hésiterai pas à soumettre mes prochains doutes sur le forum !

Bonne fin de journée