Langage formel, concaténation et commutativité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 23 Mai 2014, 12:24
par Mikihisa » 23 Mai 2014, 12:24
Bonjour à tous !
J'étudie un cours intitulé "Langages & Automates" en autodidacte, et je ne peux donc pas avoir de correction lorsque je butte sur un problème. Je me tourne donc vers vous, forumeurs et forumeuses dans l'espoir que vous pourrez m'aiguiller dans la résolution de mon problème. En voici l'énoncé :

est un alphabet fini,

et

deux mots de
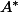
et

la concaténation.
Montrer que

si et seulement si il existe un mot

et deux entiers

,

tels que
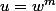
et
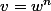
. On pourra procéder par récurrence sur

.
Alors pour je n'arrive pas du tout à voir cette fameuse récurrence. Je vois bien que si
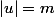
et
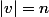
on a

et

et si
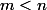
on a
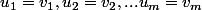
et
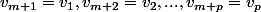
avec
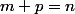
mais je n'arrive toujours pas à trouver cette récurrence.
Si vous pouviez m'aiguiller en me donnant quelques indices je vous en serai infiniment reconnaissant !
Bien cordialement.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 23 Mai 2014, 12:39
par Monsieur23 » 23 Mai 2014, 12:39
Aloha,
Comme le dit l'énoncé, faisons une récurrence sur p = |u|+|v| :
si p=0, c'est trivial.
on suppose que c'est ok pour un p, et regarde pour p+1.
On prend donc deux mots u et v tels que |u|+|v|=p+1, et tels que uv = vu.
Il faut que tu te ramènes à des mots dont la somme des longueurs vaut p.
Tu peux, si tu veux détailler, écrire
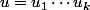
et
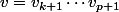
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Mikihisa
- Membre Relatif
- Messages: 242
- Enregistré le: 23 Mai 2014, 12:03
-
 par Mikihisa » 23 Mai 2014, 15:30
par Mikihisa » 23 Mai 2014, 15:30
Merci Monsieur23, j'ai finalement réussi ! En fait j'ai poser |u|;)|v|et j'ai séparer les cas :
|u| = 0 -> w=v, p=0 q=1
|u| = |v| -> w=u=v, p=q=1
0 < |u| < |v| -> comme uv=vu on a v = ux avec |x|>0, ensuite tout se fait super bien, on a uux=uxu donc ux=xu et |xu| ;) n car |u|>0, puis on conclu en appliquant l'hypothese de récurrence sur u et x et en transférant tout ca dans u et v.
Merci à toi !
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 23 Mai 2014, 15:47
par Monsieur23 » 23 Mai 2014, 15:47
Yép, ça a l'air de marcher ;-)
Bien joué!
« Je ne suis pas un numéro, je suis un homme libre ! »
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
