Langage ensembliste

[Kikoo <3 Bieber]

Non là tu décris seulement P(vide) : {vide,{vide},{vide},...,{vide}} = {vide,{vide}} = P(vide)
Si un ensemble X est fini et contient k éléments, combien d'éléments y a-t-il dans P(X) ?

Salut Doraki !
Il y en a

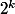
[Kikoo <3 Bieber]

Je ne comprends pas trop ton ensemble qui contient des singletons répétés.

Essaye de trouver P(vide) déjà, puis P(P(vide)) etc. Que peux-tu dire aussi de Card(P^n(vide)) ?

Salut Nightmare,

J'ai P(vide)={vide}
P(P(vide))={vide,{vide}}
Hmmm, désolé chuis pas trop réactif j'arrive pas vraiment à me représenter la chose.

[Doraki]

Quand on veut faire un calcul, on peut toujours le faire à l'aveugle sans se représenter quoi que ce soit.
D'ailleurs je suis pas sûr qu'il y AIT un truc à se représenter dans notre cas.

le prochain, P(P(P(vide))), il contient quoi ?

[Kikoo <3 Bieber]

Quand on veut faire un calcul, on peut toujours le faire à l'aveugle sans se représenter quoi que ce soit.
D'ailleurs je suis pas sûr qu'il y AIT un truc à se représenter dans notre cas.

le prochain, P(P(P(vide))), il contient quoi ?

Tout d'abord il a l'élément vide, puis il a {vide}, puis il a {vide, {vide}}.

[Doraki]

yup mais il te manque le 4ème et dernier élément encore.

[Kikoo <3 Bieber]

Hmmm... Ne serait-ce pas {{vide}} ?
Cette écriture me laisse un peu perplexe.

[Doraki]

Oui c'est ça. {{vide}} est l'ensemble qui contient uniquement l'ensemble qui contient uniquement l'ensemble qui ne contient personne.

[Kikoo <3 Bieber]

And my brain goes mad :marteau:

Oki, donc en fait ça devient carrément pas écrivable au bout d'un moment ? :/

[Doraki]

Ca dépend ce que t'appelles écrivable.
si tu remplaces tous les "vide" par "{}", tous ces ensembles ne sont rien de plus qu'un paquet d'accolades. C'est pas bien plus compliqué que d'écrire un grand nombre comme "5848641531587976412133"

[Luc]

And my brain goes mad :marteau:

Oki, donc en fait ça devient carrément pas écrivable au bout d'un moment ? :/

Si, mais le nombre d'éléments augmente de façon exponentielle.

[Kikoo <3 Bieber]

Ok, merci à vous, je crois que j'ai un peu mieux compris ;)

[Kikoo <3 Bieber]

Voilà une somme qui me fait "pas mal sécher" :

"Montrer que "
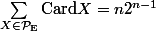
Avec E un ensemble fini de cardinal supérieur à 1.

PS : j'ai déplacé ce post d'un autre topic pour ne pas le polluer.

[Luc]

Voilà une somme qui me fait "pas mal sécher" :

"Montrer que "
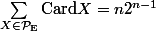
Avec E un ensemble fini de cardinal supérieur à 1.

PS : j'ai déplacé ce post d'un autre topic pour ne pas le polluer.

Tu as essayé quoi?

[Kikoo <3 Bieber]

Ben en fait je vois que le cardinal de X varie de 0 à n. Or un ensemble à n éléments possède sous-ensembles, mais après je vois pas comment approcher la somme.

Edit : Bon je vois que t'es en train de répondre, c'est gentil de ta part
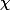
Je dois aller dormir, demain j'ai khôlle de et j'ai que dalle révisé j'ai l'impression U_U
Merci, je verrai ce que t'as mis demain !

[Luc]

Ben en fait je vois que le cardinal de X varie de 0 à n.

C'est déjà pas mal. Tu peux donc sommer sur le cardinal de X (ie tu tries les parties X de E suivant leur cardinal k). Combien y a-t-il de parties de E à k éléments?

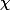
EDIT : c'est chimie? J'adorais ça en prépa. Bien plus marrant que la physique...

[Kikoo <3 Bieber]

Salut Luc !

C'est déjà pas mal. Tu peux donc sommer sur le cardinal de X (ie tu tries les parties X de E suivant leur cardinal k). Combien y a-t-il de parties de E à k éléments?

Ca me fait vaguement penser aux p-combinaisons, genre combien de parties à k éléments parmi ? J'ai jamais géré le dénombrement :/

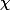
EDIT : c'est chimie? J'adorais ça en prépa. Bien plus marrant que la physique...

Oh la chimie, que c'est vilain ! Par contre la physique est ma matière préférée (outre l'optique géométrique lorsqu'on doit faire des "dessins-avec-une-règle-et-il-faut-pas-dépasser-sinon-c'est-pas-bien").

[Luc]

protip : si X est un ensemble fini à n éléments, le nombre de parties de X à k éléments vaut . C'est (ou ça devrait être) du cours.

[Kikoo <3 Bieber]

OKKKKK (chuis à l'Ouest, définitivement ^^).

Pour récapituler, je cherche à sommer les cardinaux de chaque partie de E.
Je peux commencer par regrouper les parties ayant un même nombre k d'éléments donc il s'agit des ensembles à k parmi n éléments. Puis ensuite il me reste plus qu'à sommer pour k allant de 0 à n ?

Edit : Ah mer... credi ! J'avais oublié de multiplier par k ! Je pense avoir un truc cohérent là

Donc on a non ? Ouais mais calculer ce truc c'est...

[Luc]

OKKKKK (chuis à l'Ouest, définitivement ^^).

Pour récapituler, je cherche à sommer les cardinaux de chaque partie de E.
Je peux commencer par regrouper les parties ayant un même nombre k d'éléments

Oui.

donc il s'agit des ensembles à k parmi n éléments.

Plus précisément, ce sont des parties de E à k éléments. Elles sont toutes de cardinal k, et il y en a k parmi n.

Puis ensuite il me reste plus qu'à sommer pour k allant de 0 à n ?

Oui. Mais il y a une astuce pour calculer cette somme (penser au binôme de newton et à la dérivation).

[Kikoo <3 Bieber]

Ok,

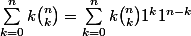
Dans l'immédiat, je vois que (je force un binôme)
Mais le k gène, donc il me faudrait une manière pour le jerter de là...