Langage ensembliste

[Luc]

Ok,

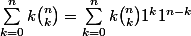
Dans l'immédiat, je vois que (je force un binôme)
Mais le k gène, donc il me faudrait une manière pour le jerter de là...

et le développement de (1+x)^n?

[SimonB]

Ok,

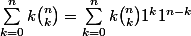
Dans l'immédiat, je vois que (je force un binôme)
Mais le k gène, donc il me faudrait une manière pour le jerter de là...

Pose et repense au conseil précédent (la dérivation).

[Kikoo <3 Bieber]

et le développement de (1+x)^n?

.
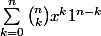
Je dérive et je trouve
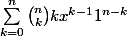
C'est bien par-là que tu veux me mener ?

[Luc]

.
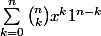
Je dérive et je trouve
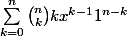
C'est bien par-là que tu veux me mener ?

Ça se rapproche pas mal de ce que tu veux calculer, non?

[Kikoo <3 Bieber]

Certes, je vois à peu près là où je dois aboutir mais j'ai jamais été doué en changements d'indices. Surtout que ce soir j'ai un peu de mal à réfléchir, pourras-tu me guider stp ?

Alors tout d'abord, je poserais l=k+1 pour me débarasser de l'indice k=0.

[Luc]

Certes, je vois à peu près là où je dois aboutir mais j'ai jamais été doué en changements d'indices. Surtout que ce soir j'ai un peu de mal à réfléchir, pourras-tu me guider stp ?

Alors tout d'abord, je poserais l=k+1 pour me débarasser de l'indice k=0.

Ok, mais pour obtenir ce que tu veux calculer, il ne faut pas de x. Donc qu'est-ce que tu as envie de faire?

[Kikoo <3 Bieber]

J'aimerais bien avoir l'exposant k-1 nul ^^

[Luc]

J'aimerais bien avoir l'exposant k-1 nul ^^

Ça c'est impossible car k-1 prend plusieurs valeurs différentes, mais on peut évaluer l'expression pour des valeurs particulières de x.