Juxtaposition de bases

[coussinblanc]

bonjour,
lorsque l'on a une base B1=(u) de G et une base B2 =(v,w) de F, si on prouve que la famille ( u,v,w) obtenue en juxtaposant les bases B1 et B2 est une base de IR^3, alors peut-on conclure quand à la supplémentarité de F et G dans IR^3?

[GaBuZoMeu]

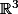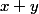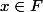Il suffit de voir que tout élément de , s'écrit, et de manière unique, sous la forme avec et 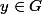. Ça ressort immédiatement de la définition de base.
Le même argument marche aussi pour plus de deux sous-espaces : si en mettant bout à bout des bases de ces sous-espaces on obtient une base de l'espace total, alors cet espace est la somme directe des sous-espaces.