Jouons au chat et à la souris

par **Nightmare** » 17 Juin 2009, 17:14

Bonjour :happy3:

Encore un exercice de ma conception, pas vraiment difficile, si vous voulez vous amuser :

Mme Souris se baladait bien tranquillement lorsque elle vit en face d'elle M le Chat, apparemment affamé.

Bien évidemment, Mme Souris n'a qu'une solution, rejoindre son trou, situé à 50m sur sa droite (De sorte que le triangle Trou-Souris-Chat soit rectangle). Elle se mis alors à courir à une vitesse constante vers ce dernier.

M le Chat, dès l'instant où son diner se mis à fuir se lança à sa poursuite, se dirigeant constamment dans sa direction avec une vitesse 2 fois plus importante que son repas.

Question :

Montrer que la survie de la souris ne dépend uniquement que de sa distance initiale avec le chat. Quelle doit être au minimum cette distance pour que la souris soit sure de vivre ?

Bon courage pour essayer de sauver Mme Souris.

:happy3:

par **fourize** » 18 Juin 2009, 19:30

bonjour Nightmare
et bravo t'es au 6000 message lol

* pour ton exo; il est bien plus de physique que de maths !
je touve 50 la distance que doit separer le chat et la souris
pour que cette dernière survie !
après ta confirmation je te dirais comment j'ai fait !

par **Nightmare** » 18 Juin 2009, 19:31

Salut :happy3:

Hum je ne trouve pas 50 ! cela dit tu peux poster ta méthode voir où est ton erreur (ou la mienne :lol3: )

par **fourize** » 18 Juin 2009, 19:47

re,

Nightmare a écrit:Salut :happy3:
Hum je ne trouve pas 50 ! cela dit tu peux poster ta méthode voir où est ton erreur (ou la mienne :lol3: )

avant de demontrer que la survie de la sourie depend de la distance qui la separt avec le chat. commençons par une intrpretation:

comme la sourie s'enfuit avec une vitesse V (disons v= 50m/h) et le chat
2V ( donc 100m/h) si le triangle est isocel rectangle en (soris). le chat la rattrape exactement au trou ! (i.e survie car le chat ne peut entrer ! )

t'es bien d'accord ?!

par **Nightmare** » 18 Juin 2009, 20:48

Attention, tu oublies un point important de l'énoncé : Le chat se dirige constamment vers la souris, sa trajectoire est donc loin d'être rectiligne.

par **Nightmare** » 05 Juil 2009, 18:02

Personne n'a trouvé? La seule "difficulté" est de modéliser correctement le problème. Ensuite, c'est une "simple" équadiff à résoudre.

par **Zavonen** » 05 Juil 2009, 20:29

Poser l'équation n'est pas difficile:
Dans un repère ayant pour origine la position intiale de la souris, la souris se déplace sur l'axe Ox en direction de son trou à vitesse constante k.
L'équation de son mouvement est donc:
x(t)=kt
y(t)=0

Pour ce qui concerne le chat,, soit (X(t),Y(t)) sa position à l'instant t.
On a deux données à traduire:
La vitesse (absolue) est double de celle de la souris:
X'²+Y'²=4k²
Le chat court toujours en direction de la souris:
Le vecteur vitesse est colinéaire au vecteur joignant la position du chat à celle de la souris, on peut annuler un déterminant:
YX'-Y'(X-kt)=0
On joint les conditions initiales:
X(0)=0
Y(0)=h (distance initiale du chat à la souris)
On obtient un système d'équadiffs du premier ordre à deux inconnues. Malheureusement il n'est pas du premier degré. Il doit y avoir une astuce pour éliminer les carrés mais laquelle ???
Je ne pense pas que l'équadiff soit si facile que cela à résoudre.
Une fois qu'elle est résolue il n'y a plus qu'à étudier le minimum de (X(t)-kt)²+Y(t)² qui sera fonction de h et ajuster h pour que ce minimum soit nul.

par **Zavonen** » 05 Juil 2009, 20:34

Il y a là quelque chose d'intéressant
Mais hélas, il s'agit d'un chien qui poursuit un lièvre :cry:

par **Ysengrin** » 08 Juil 2009, 16:48

J'y réfléchirai en soirée (j'ai internet qu'au bureau) mais je pense qu'il ne faut pas s'interresser aux vitesse parce que c'est la trajectoire qui compte (la trjectoire de la souris est rectiligne on l'assimile à l'abscisse celle du chat fait comme une fonction genre distance initiale du chat à la souris moins exp(2t-50)
ou t est la position de la souris par rapport à celle de départ.(j'ai pris t exprès genre vitesse-position-temps tout ça ..)

La trajectoire du chat va -t-elle rejoindre celle de la souris soit l'abscisse (gloups! :triste: ) ?

C'est pas la solution car ça manque de rigueur mais je pense qu'on peut trouver comme ça .
bonne soirée ^_^

par **Ysengrin** » 09 Juil 2009, 08:15

Bonjour,
bon en fait c'est plus compliqué que prévu :doh:
je penche plutôt une trajectoire de type

-

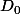
(dérivée égale à 2v)
bon j'y réfléchirai avec une feuille de papier ce soir

(marrant quand mm ce problème)

par **Black Jack** » 09 Juil 2009, 09:21

Je trouve que le minet doit être à une distance initiale minimum de 75 m par rapport à la souris, pour que celle-ci échappe au croquage.

:zen:

Jouons au chat et à la souris

Jouons au chat et à la souris

Qui est en ligne