Jolie intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 19 Juin 2010, 23:10
par Ludo1be » 19 Juin 2010, 23:10
Bonjour,
Je dois résoudre cela:

Je pose donc x = cos t?
Donc x' = -sin t
Ca me fait:

=
Etant donné la racine, on ne peut pas avoir une tan²? Juste?
Ca me fait:

Maintenant je peux poser
s = cos t
s' = -sin t
Ca me fait:

Mais ca tourne en rond... :/
Une aide svp?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Juin 2010, 23:21
par fatal_error » 19 Juin 2010, 23:21
salut,
pour cos(t)/sin^2(t), on peut supposer que 'la' primitive a la gueule de
sin^(-1) (t), comme ca quand on dérive on a du sin^(-2)(t), et la fonction dérivée 'composée' qui sort c'est cos(t) et ca arrange bien
la vie est une fête

-
Ludo1be
- Membre Relatif
- Messages: 220
- Enregistré le: 20 Juil 2009, 09:11
-
 par Ludo1be » 19 Juin 2010, 23:23
par Ludo1be » 19 Juin 2010, 23:23
fatal_error a écrit:salut,
pour cos(t)/sin^2(t), on peut supposer que 'la' primitive a la gueule de
sin^(-1) (t), comme ca quand on dérive on a du sin^(-2)(t), et la fonction dérivée 'composée' qui sort c'est cos(t) et ca arrange bien
Heuuuu... Tu peux être plus explicité? O_o
Je ne vois déjà pas de cos(t)/sin^2(t)
 par busard_des_roseaux » 20 Juin 2010, 06:02
par busard_des_roseaux » 20 Juin 2010, 06:02
Bj,
au voisinage de x=0, l'intégrande est positive et l'on peut écrire
un équivalent

l'intégrale étudiée est de même nature que
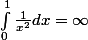
l'intégrale est divergente . pour s'en convaincre
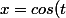)
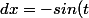dt)
 \over cos^2(t)} dt = [tan(t)-t]_{t=0}^{\frac{\pi}{2}}=\infty)

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 20 Juin 2010, 07:13
par fatal_error » 20 Juin 2010, 07:13
re,
alors dans l'ordre :
cos(t)/sin^2(t)
tu remplace cos par sin et sin par cos...
Edit pour la fin : pas vu que le dx avait pas été fait
la vie est une fête

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités




