Joli exo

[B_J]

Bonjour ;
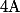
Soit une matrice definie positive d'ordre
calculer
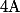
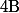
en deduire que si et sont deux matrices symetriques reelles definies positives et si alors

PS: je connais la reponse

[Joker62]

L'exposant dans l'exponentielle c'est :

non ? avec

[B_J]

Salut Joker62
oui c'est bien ca
on peut l'ecrire dans une base bien choisie sous la forme ...

[B_J]

Ne pas oublier de multiplier par le jacobien correspondant au chagement de base
on peut utiliser le resultat suivant

[Daniel-Jackson]

Bonjour ;
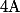
Soit une matrice (symétrique ? )definie positive d'ordre
calculer

PS: je connais la reponse

Parce que si la matrice est symétrique (elle se diagonalise) définie positive (entraine l'existence de l'intégrale) et (par Fubini-Tonelli) on aura des produit de la gaussienne à integrer donc des racine de Pi avec les lamdas (les valeur propres) ....

[B_J]

Salut Daniel
la matrice peut ne pas etre symetrique

[Daniel-Jackson]

Salut Daniel
la matrice peut ne pas etre symetrique

Ok ça serait trop facile aussi :stupid_in

EDIT: Oui en fait on écrit la forme dans une base orthogonale et tout s'en suit...comme l'a fait jocker je vois à peu près ce qu'il faut faire .
En fait on diagonalise plutot la forme que la matrice ...... ok :id:

[B_J]

on pourra suivre les indications que j'ai données ( cf messages #3 et #4 )

[Joker62]

Ben dans une base orthonormale, elle est semblable à une matrice diagonale avec les valeurs propres lambda toutes positives.

Le Jacobien associé c'est la matrice du changement de base :^) ???
J'vois pas trop :^)

[B_J]

on a un changement de coordonnées linéaire donc le ja cobien vaut
rq: le jacobien est un determinant ( donc un nombre )

[Joker62]

Alors on a n forme linéairement indépendantes oui.

Donc la jacobienne est composée en ligne des coefficients suivant les x_1 , ... x_n
J'ai jamais vu que le déterminant d'une telle matrice vaut 1...
Etrange...

[fahr451]

si X = P X ' est le changement de base
la jacobienne est P son déterminant est det P qui ne vaut a priori pas 1 c'est vrai si P est orthogonale (cas où A est symétrique donc ortho diagonalisable)

si A n'est pas symétrique

A = S + B avec S symétrique B antisymétrique et

tXAX = tXSX

[Joker62]

Bon donc sinon en supposant A symétrique

l'intégrale vaut :

[B_J]

Salut ;

Bonjour ;
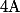
Soit une matrice definie positive d'ordre
calculer

Il existe une base orthonormée et des réels tels que la forme quadratique s'ecrive dans cette base :
. Le jacobien correspondant au changement de coordonnées linéaire valant , l'integrale s'écrit :

compte tenu de
il vient :

[fahr451]

quel est le lien entre les lambda i et det A lorsque A n'est pas symétrique ...?

[B_J]

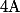
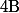
en deduire que si et sont deux matrices symetriques reelles definies positives et si alors

si ou il n'y a rien a montrer.
sinon , d'après ce qui precede on a :
( inégalité de Holder ) d'ou ...