Jeux defi
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 19 Déc 2006, 12:47
par yos » 19 Déc 2006, 12:47
C'est bien; la solution est dans ce goût là.
-
Yipee
- Membre Relatif
- Messages: 256
- Enregistré le: 15 Déc 2005, 07:34
-
 par Yipee » 19 Déc 2006, 20:50
par Yipee » 19 Déc 2006, 20:50
Dans le même genre d'idée, on voit en utilisant que
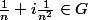
que
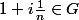
d'où
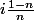
On a alors aussi
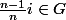
et finalement en faisant la diiférence de deux tels termes pour n et n+1 que iQ est inclus dans G. Je pense que le même genre de calculs donne que Q est aussi dans G. Par contre, je n'ai pas d'idées pour continuer.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 20 Déc 2006, 06:02
par tize » 20 Déc 2006, 06:02
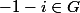
donc pour tout
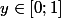
,
+(y^2-1)i \in G)
.
De plus, pour tout
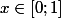
il existe
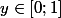
(
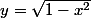
) tel que
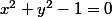
(le cercle...), et on a alors :
 +i(x^2+y^2-1)=x+y-1=x+\sqrt{1-x^2}-1 \in G)
pour tout
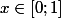
or cet ensemble d' x avec leurs opposés contient une partie ouverte non vide de

contenant 0 et donc par dilatation
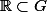
.
De même, on montre que
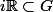
et par addition
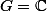
J'ai bon ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Déc 2006, 08:56
par yos » 20 Déc 2006, 08:56
Bravo Tize.
Un peu plus simple :
pour tout x de [0,1],
^2)-(x+ix^2))
,
donc [0,1] inclus dans G.
Et on achève facilement.
A toi de poser une question. Tu peux créer un fil "défi 2" peut-être.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 20 Déc 2006, 10:24
par tize » 20 Déc 2006, 10:24
A oui effectivement, c'est beaucoup plus simple comme ça :id:
Je vais créer un nouveau fil défi 2 !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
