Jeux defi

par **BQss** » 15 Déc 2006, 06:15

Je vous propose un petit jeu.
Il faut poser une question ou un probleme. Le premier qui repond juste(celui qui a posé la question devra a chaque fois arbitrer)
marque un point. Mais surtout c'est a celui qui a bien repondu de poser alors une nouvelle question.

Et ainsi de suite, chaque nouvelle reponse donnant lieu a une nouvelle question.

J'initie le jeu avec une petite question assez facile:

QUESTION:
On connait tous des fonctions Lebesgue integrable qui ne sont pas Riemann integrable( la fonction indicatrice sur les irrationnels par exemple).
Je demande le contraire:
Donner la limite convergente de l'integrale d'une fonction Riemman integrable(donc une integrale impropre) qui n'est pas Lebesgue integrable.
En d'autre terme, trouvez une integrale impropre convergente mais qui n'est pas lebesgue integrable.
Avec la justification evidemment.

Je ne pense pas que la question va rester longtemps, mais bon, au moins le jeu va prendre comme ca

.

par **Yipee** » 15 Déc 2006, 08:18

OK, j'y vais.

Il suffit de prendre une intégrale semi-convergente. Par exemple

Il est bien connu qu'elle converge (faire une intégration par partie), cependant, elle n'est pas absolument convergente. En effet elle est "supérieure" à la série

Cette dernière diverge.

par **BQss** » 15 Déc 2006, 15:54

Yipee a écrit:OK, j'y vais.

Il suffit de prendre une intégrale semi-convergente. Par exemple

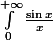
Il est bien connu qu'elle converge (faire une intégration par partie), cependant, elle n'est pas absolument convergente. En effet elle est "supérieure" à la série

Cette dernière diverge.

Ok, tu as le point et c'est a toi de poser la question.

Mais j'aimerai que les gens justifie plus.
Par exemple, pour montrer que l'integrale généralisée converge, montre moi quan dmeme que tu coupes en deux [0;1] et ]1;+inf[ par exemple que tu utilises l'equivalence de sinx/x qui est une fonction positive sur [0;1] puis que tu integres par parties sur ]1;+inf[ et enfin que tu majores la valeur absolue de cosx/x^2 pour en deduire que le membre sous l'integrale est absolument convergent et donc vconvergent.

Pour la serie je suis d'accord celle de gauche diverge, mais l'integrale est sur ]0;+inf[, et ta somme ommet l'integrale de [0;pi/6], donc il reste quelquechose a rajouter c'est a dire majoré l'integrale sur [0;PI/6](meme si c'est facile] vu que ca converge il faut quand meme le mettre pour etre rigoureux en rajoutant une constante de chaque coté de l'inégalité. J'aurais aussi aimé que tu me montres comment tu as majoré la somme de droite, c'est a dire que tu indiques que tu as probablement minoré la fonction positive(car la valeur absolue que tu n'as pas mise d'ailleurs)qui est donc continue sur l'intervalle par sa borne inf ou quelquechose du genre.

En fait moi, j'avais comme exemple tout simplement:
integrale (sin(x)) de -inf à +inf .

L'integrale généralisée vaut lim n-->+inf de integrale(sinx) de -n à +n= donc lim de (0) car sin(x) est une fonction impaire.
Et lim (0) vaut 0 donc l'integrale converge.

Or elle n'est pas absolument convergente, donc elle n'est pas lebesgue integrable. Car lim somme_sur_k integrale |sin(x)| sur [kpi/2;(k+1)pi/2] par exemple = lim quand k-->+inf de (k) = +inf.

De maniere generale il suffit de prendre l'integrale d'une fonction impaire dont la partie superieure a 0 et celle inferieure a 0 diverge.

Yipee c'est a toi de poser une question maintenant.
Tu devras arbitrer la reponse, soit exigent c'est le but, la reponse ne doit etre accordé que si la justification est juste.

par **fahr451** » 15 Déc 2006, 15:56

l 'intégrale de sin entre moins l 'infini et plus l 'infini n 'existe pas

car celle entre 0 et plus l 'infini n 'existe pas .

par **BQss** » 15 Déc 2006, 16:01

fahr451 a écrit:l 'intégrale de sin entre moins l 'infini et plus l 'infini n 'existe pas

car celle entre 0 et plus l 'infini n 'existe pas .

Non c'est la limite de l'integrale de sin(x) entre -n et n
c'est a dire l'integrale généralisée:
integrale (sin(x)) entre -inf et +inf définie comme la limite de l'integrale de -n à n

car celle entre 0 et plus l 'infini n 'existe pas-->
ca ne marche pas:
c'est comme si tu me disais l'integrale de la serie de terme (-1)^n/n diverge car la serie de terme 1/n diverge. Cette serie n'a effet pas de limite si on separe les termes positifs et negatifs en les sommant dans un ordre ou viennent d'abord les termes positifs par exemple. D'ou l'importance de l'ordre de sommation, dans la theorie de lebesgue cette somme est divergente pour la mesure de comptage par exemple... Alors que si on somme normalement la serie alternée (-1)^n sur n omme la limite de la serie de 0 à n de (-1)^n elle converge biensur.

Tout depend de l'ordre de sommation et quand on fait l'integrale généralisé(ce b'est pas comme lebesgue), on definit en fait la lmite d'une integrale de Riemann.
On fait donc ici lim entre -n et n et et c'est donc lim de 0 qui vaut 0.

Cela divergerait si on definissait l'integrale geralisé entre -inf et +inf de la sorte:
lim quand n,m tende vers +inf de integrale (sinx) de -n à +m, la oui l'integrale n'existe pas. Mais ce n'est pas comme ca que j'ai définie mon integrale...
J'ai définie mon integrale de -n à n...

par **fahr451** » 15 Déc 2006, 16:03

BQss a écrit:Non c'est la limite de l'integrale de sin(x) entre -n et n
c'est a dire l'integrale généralisée:
integrale (sin(x)) entre -inf et +inf définie comme la limite de l'integrale de -n à n

non tu te trompes

par **BQss** » 15 Déc 2006, 16:06

fahr451 a écrit:non tu te trompes

Regarde ce que j'ai mis.

par **fahr451** » 15 Déc 2006, 16:09

la limite qd n tend vers plus l infini de l 'intégrale de sin entre -n et n vaut 0 nul ne le conteste
MAIS l intégrale entre moins l 'infini et plus l infini de sin N EXISTE PAS

ds une intégrale généralisée pour regarder la convergence ( l' existence) il faut SEPARER les "problèmes".

par **BQss** » 15 Déc 2006, 16:20

fahr451 a écrit:la limite qd n tend vers plus l infini de l 'intégrale de sin entre -n et n vaut 0 nul ne le conteste
MAIS l intégrale entre moins l 'infini et plus l infini de sin N EXISTE PAS

ds une intégrale généralisée pour regarder la convergence ( l' existence) il faut SEPARER les "problèmes".

Ah, et donc c'est un probleme de definition?
j'ai pourtant une definiton que j'ai toujours employé qui dit qu'on appelle integrale sur [a;b[ lorsqu'elle existe la limite de la fonction qui a x associe l'integrale de Riemann entre a et x quand x tend vers b.

La question est donc que se passe-il quan dl'intervalle est ]-b;b[...
Pour moi ca devient lim de la fonction qui a x associe l'integrale de Riemann entre -x et x quand x tend vers b.
et pour toi cela devient lim quand n tend vers b et m tend vers b, auquel cas cela n'a pas de limite... Vu qu'on si on fait tendre n et m differamment vers b ca n'a pas de limite et donc la limite n'existe pas.

Pourtant je ne vois pas pas au non de quoi on ne ferait pas tendre de part et d'autre par le meme parametre... Si on utilise la definition de la limite de l'integrale de Riemann sur un intervalle simetrique lorsqu'il s'agit d'une fonction impaire comme la definition d'une integrale impropre...

par **fahr451** » 15 Déc 2006, 16:23

voila c 'est une définition
la définition initiale f [a,b[ ne traite que du pb en b
ensuite si c' est ]a,b[ il faut fixer c entre a et b strictement ( c qq ) et regarder SEPAREMENT ]a,c] et [c,b[ et
l intégrale entre a et b existe SSI les deux intégrales existent .
le choix de c n 'intervenant pas.

par **BQss** » 15 Déc 2006, 16:36

fahr451 a écrit:voila c 'est une définition
la définition initiale f [a,b[ ne traite que du pb en b
ensuite si c' est ]a,b[ il faut fixer c entre a et b strictement ( c qq ) et regarder SEPAREMENT ]a,c] et [c,b[ et
l intégrale entre a et b existe SSI les deux intégrales existent .
le choix de c n 'intervenant pas.

Oui mais tu l'as ecrit toi meme si c'est ]a;b[, mais moi c'est ]-b;b[, donc oau non de quoi tu ne fais pas tendre de la memem maniere les b.
C'est normale qu'on separe le a et le b vu que de toute facon c'est deux limite differente. En quelque sorte c'est une fonction de deux variables.
Mais si les bornes utilises le meme parametres... C'est le sense de ce que j'ai ecrit plus haut, toi tu traites b et -b comme de parametres differents, comme si tu t'attaquait a un intervalle ]a;b[ quelquonque... D'oul e fait qu'on separe les limites vu que de toute facon cela revient strictement aux meme car on fera tendre deux parametres differents.

Quand on separe d'habitude, on le fait naturellement parce que cela revient au meme, mais rien ne t'empeche d'ecrire:
integrale sur ]a;b[=
lim integrale quand x-->a et y-->b de integrale de x a y de f(u), ce qui revient a séparé les inetgrales.
Par contre si c'est de ]-b;b[ il n'y a plus qu'un parametre et donc il n'y a plus de raison de prendre deux variables.

Est ce que tu pourrais me montrer un lien ou quelquechose ou on traite un intervalle simetrique ou un intervalle du type ]g(x);f(x)[.
Comment traite tu une integrale généralmisée sur une intervalle de la forme ]g(x);f(x)[ quand x-->a ?
Est ce que tu es sure que tu ne confonds pas la methode habituel qui est de sistematiquement coupé l'integrale en deux quand il y a deux borne avec le fait qu'on est obligé de faire comme ca, auquel cas je peux definir la lim d'une integrale de -x à x comme l'integrale de -inf a +inf?

par **Yipee** » 15 Déc 2006, 16:38

fahr451 a raison pour la définition des intégrales "doublement impropres".

Bon, c'est à moi, voici la question (c'est ce que j'ai eu à l'oral de l'ENS) :
Soit f une application de R dans

montrer que son image est d'intérieur vide.

Edit (merci fahr451) : on suppose que f est

par **fahr451** » 15 Déc 2006, 16:39

tu as parfaitement le droit de manipuler un objet s 'ils existe

lim intégrale(bornes -n ,n) de sin mais tu n 'as pas le droit de dire que cet objet est égal à un autre objet (intégrale de -inf à + inf) que TOUS ( sauf toi) s 'accordent à définir autrement.

par **fahr451** » 15 Déc 2006, 16:43

-> yipee aucune hypothèse sur f ?

par **Yipee** » 15 Déc 2006, 16:45

Oups, oui, j'ai oublié C^1... Bien sur sinon c'est faux : je modifie le message initial

par **fahr451** » 15 Déc 2006, 16:46

continue ou c1 ?

par **Yipee** » 15 Déc 2006, 16:47

Avec uniquement continue c'est faux.

par **BQss** » 15 Déc 2006, 16:47

fahr451 a écrit:tu as parfaitement le droit de manipuler un objet s 'ils existe

lim intégrale(bornes -n ,n) de sin mais tu n 'as pas le droit de dire que cet objet est égal à un autre objet (intégrale de -inf à + inf) que TOUS ( sauf toi) s 'accordent à définir autrement.

ok, bon.

Bonne chance pour la prochaine question, j'y vais les gars a+.

par **fahr451** » 15 Déc 2006, 17:35

sinon il existerait x réel tel que df(x) surjective ?

par **yos** » 15 Déc 2006, 18:45

Si f(R) contenait un ouvert, le théorème d'inversion locale serait mis à mal.

Jeux defi

Jeux defi

Qui est en ligne