Jensen.

[polka-dots]

Bonsoir,

une correction que je ne comprends pas, et qui concerne l'égalité de Jensen.

J'ai précédemment montrer que ln(1+) était convexe. La seconde question est la suivante:

En déduire que pour toute famille finie: (x1,x2,..,xn) de réels strictement positifs:

1+ Pourquoi à la place des xn, on a ln(xn)?
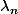
-> Pourquoi les coefficients sont égaux à 1/n?

Merci d'avance.

[Finrod]

-> Pourquoi à la place des xn, on a ln(xn)?
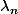
-> Pourquoi les coefficients sont égaux à 1/n?

Les xn sont des points génériques. Tu peux aussi appliquer Jensen avec yn=ln(xn) , ça ne pose aucun problème, les yn forment otujours une famille de n pts.

Pour ta 2ème question, c'est parce que c'est le choix le plus simple et qu'il marche. D'ailleurs, c'est aussi le choix le plus courant en exo.

[polka-dots]

ah ouais mais j'aurais pas eu la correction, j'y aurait pas du tout pensé. Bon ok, merci.

Y a deux passages que jcomprends pas (on passe au produit, et ça jlai jamais vu):

on me dit que ça équivaut à:

ln(1+)<<

Le passage en gras je ne le comprends pas

Et je ne comprends pas non plus ceci:

=

[Finrod]

Dans la premier expression, il me semble qu'il faut juste écrire .

Dans le second, ce n'est pas la somme qui est égale au produit mais l'exponentielle de la somme.

[Finrod]

Dans la première expression, on prend aussi l'exp de la somme à gauche. C'est ça qui te posait problème il me semble.

[polka-dots]

Désolé, pour les deux, j'arrive pas à comprendre ce que tu veux dire.

ln(1+)

J'vois pas cmoment on passe d'une somme à un produit?

[polka-dots]

J'mets le "développement" en entier, ce sera plus compréhensible:

ln(1+<<

ce qui équivaut à :

ln(1+)<<

et donc à:

ln(1+)<<

et donc a:

1+<<

[polka-dots]

La 1, je l'ai comprise, jsuis bète T.T

[Finrod]

L'exponentielle d'une somme est tjrs un produit.



C'est valable pour toute somme finie.

[polka-dots]

Merci! C'est bien plus clair.