Isomorphisme entre sous groupe de GL2(R) et GL2(F2)

[OscarLacoste]

Bonjour, j'essaye de me remettre à jour en théorie des groupes pendant ces grandes vacances (donc vous risquez de me voir souvent sur ce forum ), et en ce moment je bloque sur comment montrer l'isomorphisme entre le sous groupe de GL2(R) formé par les matrices suivantes :



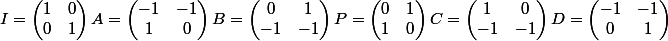
et GL2(F2)

Merci pour votre lecture et votre future aide!

[GaBuZoMeu]

Bonsoir,

Il n'est pas évident a priori que les six matrices données forment un sous-groupe de . Mais une fois que ceci est vérifié, on peut réduire modulo 2 (ça préserve bien le produit de matrices).

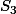
On peut voir aussi que ces groupes sont isomorphes au groupe symétrique . Comme groupe non commutatif d'ordre 6, on n'a pas trop le choix. Pour les matrices réelles, tu peux regarder la façon dont elles agissent sur l'ensemble des trois droites vectorielles , , .

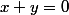
[OscarLacoste]

Oui j’ai vérifié que c’était un sous groupe en écrivant la table et inversant chaque matrice,
Du coup est ce que je peux noter que c’est isomorphe car on a l’isomorphisme (si je note H le sous groupe composé des matrices qu’on a)



est ce que c’est noté rigoureusement? est ce que ça marche?

[GaBuZoMeu]

À toi de vérifier !

[OscarLacoste]

Oui, ça marche, je savais juste pas si on pouvait noter une matrice modulo (Amod2) au même titre qu’un entier (kmod2)

Merci pour ton aide GaBuZoMeu

[GaBuZoMeu]

Pour une matrice à coefficients entiers, oui.