Isométrie affine

[mehdi-128]

Bonjour,

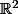
Soit le triangle de de sommets , et

Soit la symétrie orthogonale d'axe

Je cherche l'ensemble des points :

Sur un schéma c'est évident mais je vois pas comment le démontrer

[Mimosa]

Bonjour

Il suffit de trouver les symétriques des sommets, puisque pour une fonction affine f, on a f([A,B])=[f(A),f(B)]pour tout segment [A,B].

[mehdi-128]

Merci Mimosa

Je trouve que a pour sommets :

On a : et

Alors :

Donc cet ensemble est le segment

Et si je veux faire la même chose pour la rotation de centre O et d'angle ?

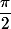
Je sais que cet ensemble sera un point. Il faut suivre la même méthode ?

[Mimosa]

Ta conclusion est fausse!

[mehdi-128]

J'ai fait une erreur de calcul je corrige :

c'est ça ?

[Mimosa]

Non

[mehdi-128]

J'ai pas compris le souci alors

[pascal16]

la symétrie d'axe y=0, c'est bien la symétrie d'axe (Ox) donc (0,0) et (0;1/2) sont invariants

[mehdi-128]

Bah c'est ce que j'ai écrit non ?

[pascal16]

Mimosa, où est-ce que ça cloche ?

[Mimosa]

Il cherchait s(M). Or le troisième sommet doit être pris en compte, et s(1/2,1/2)=(1/2,-1/2). L'image d'un triangle est un triangle!

[pascal16]

moi je comprends "les point du triangles tels que leur image est un point du triangle"

en particulier, les médiatrices laissent aussi globalement invariant 2 points

[Mimosa]

> pascal16 Tu as peut-être raison. En fait j'avais déjà vu sur un autre site de longs développements sur ce sujet, ce qui fait que j'ai été un peu vite!