Bonjour,
J'aimerais évaluer n en fonction de a et k de façon à ce que l'inégalité ci-dessous soit vérifiée, mais je n'arrive pas à isoler n. Les variables a, n et k sont des entiers naturels.
n^(k+1) - (n-1)^(k+1) < a^k
Pouvez-vous m'aider?
Merci à l'avance!
Isoler une variable
10 messages
- Page 1 sur 1
Re: Isoler une variable
Merci GaBuZoMeu,
Je connais cette identité remarquable, mais cela ne me permet pas d'isoler n. Une majoration ou minoration demeure une approximation.
Je connais cette identité remarquable, mais cela ne me permet pas d'isoler n. Une majoration ou minoration demeure une approximation.
Re: Isoler une variable
n est un entier naturel dans ton problème. Ce que je te suggère permet de déterminer très facilement un entier n tel que n ou n+1 soit le plus grand entier satisfaisant l'inégalité. Il ne te reste plus qu'à vérifier si n+1 satisfait l'inégalité, et tu as ta réponse.
Pas heureux avec ça ?
Pas heureux avec ça ?
Re: Isoler une variable
Pas heureux car je ne comprends pas ce que tu veux dire. Il faudrait illustrer par un exemple peut-être.
Merci!
Merci!
Re: Isoler une variable
Ne devines-tu pas quelle majoration et quelle minoration de +\cdots+(n-1)^k) j'ai en vue ?
j'ai en vue ?
Indication : la majoration fait intervenir et la minoration
et la minoration 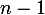 .
.
Indication : la majoration fait intervenir
Re: Isoler une variable
@GaBuZoMeu
a doit être supérieur à 1 et k doit être supérieur à 0 .
Ceci étant ,pour certains couples (a,k) le plus grand n est^{\frac{1}{k}}}\right]) , et pour d'autre couples on peut l'augmenter de 1 . As tu réussi à trouver un critère discriminant ?
, et pour d'autre couples on peut l'augmenter de 1 . As tu réussi à trouver un critère discriminant ?
L'inégalité est toujours vérifiée dans le premier cas . C'est le travail d'abc que de le démontrer .
a doit être supérieur à 1 et k doit être supérieur à 0 .
Ceci étant ,pour certains couples (a,k) le plus grand n est
L'inégalité est toujours vérifiée dans le premier cas . C'est le travail d'abc que de le démontrer .
Re: Isoler une variable
Merci GaBuZoMeu!
J'ai utilisé k(n-1)^k comme minorant et kn^k comme majorant et j'obtiens que n-1 < (a/(k^(1/k)) < n.
J'ai utilisé k(n-1)^k comme minorant et kn^k comme majorant et j'obtiens que n-1 < (a/(k^(1/k)) < n.
Re: Isoler une variable
Oui c'est vrai et j'obtiens alors le même résultat que Tournesol.
Merci à vous deux!
Merci à vous deux!
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
