Irréductibilité

[Ncdk]

Bonsoir,

Une chose m'échappe sur les éléments irréductibles d'un anneau commutatif intègre.

Si je me trompe pas dans la définition :

Soit non nul et non inversible. est irréductible signifie que implique que ou .
Qu'en est-il si et ?


De plus, c'est exactement pareil si on se place dans l'anneau des polynômes non ? En gros la définition reste la même sauf que nos éléments sont des polynômes ?

[zygomatique]

salut

c'est quoi A puissance X ?

[Ben314]

Salut,
C'est quoi ?
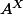
Sinon, la définition contient un "ou", qui, comme systématiquement en math. est un ou inclusif.
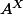
C'est à dire que, si pour un a donné, tu pouvait écrire a=bc avec b et c dans ton ça ne constituerais nullement une preuve que a est non irréductible.

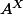
Sauf que, si ton désigne l'ensemble des inversible de A alors ce cas de figure ne risque pas de se produire vu que a étant supposé non inversible, il ne risque pas de s'écrire comme produit de deux inversibles !!!!

Ensuite, effectivement, et on va dire poliment que c'est "assez fréquent" en math : si on te donne une définition ou un théorème concernant, de façon générale, les anneaux commutatif unitaires, alors, quand tu as un anneau commutatif unitaire particulier sous la main, ben tu peut utiliser la définition et/ou le théorème.
Donc un truc valable dans tout anneau commutatif unitaire, c'est à fortiori valable dans l'anneau commutatif unitaire des polynômes à coeff. sur un corps K.
Par exemple, je vais t'en apprendre une bien bonne : un théorème comme le T.A.F. qui te dit "quelque soit la fonction continue f.....", ben lorsque tu as un cas particulier de fonction continue f, tu peut tout à fait utiliser le T.A.F. sur cette fonction là.
De même, (mais là, je sais pas si tu va me croire), le fait que a(b+c)=ab+bc pour tout réels a,b,c, ben ça marche même avec 3(5+2)=3x5+3x2. Étonnant, non ?

Tu en as d'autre des question intelligente comme ça ?

[Ncdk]

c'est les inversibles de A, je sais pas comment on le note habituellement, du moins en TeX, alors j'ai improvisé

Ah oui je vois, merci Ben pour la première partie de ton message, je vois oui.

Par contre pour le reste, je me demande car en fait je vois sur internet différente définition (équivalente j'en doute pas) de polynôme irréductible, par contre, ce qui change c'est dans quoi vivent les coefficients des polynômes, est-ce que c'est un anneau, est-ce que c'est un corps, c'est cette subtilité qui me chagrine.

Du coup j'en reviens à ce que je voulais savoir, c'était de parler sur : Les polynômes irréductibles à coefficient dans un anneau commutatif intègre et les polynômes irréductibles à coefficient dans un corps.

Il y a bien des différences non ? Parce-qu'un corps c'est cas particulier d'anneau, mais tout anneau n'est pas un corps, c'est-ce que j'avais en tête pour me poser la question sur les différences

[Ben314]

Là, effectivement, ça devient plus intéressant comme question.

- Pour définir les structures "usuelles" sur A[X] (i.e. l'addition, le produit), il suffit effectivement que A soit un anneau.
- Pour que A[X] soit commutatif (respectivement unitaire), il faut que A le soit.
- Pour pouvoir définir par exemple la dérivation, il faut aussi (au minimum) que A soit unitaire de façon à avoir un morphisme de Z dans A permettant de "multiplier" les polynômes par des entiers. Et évidement, si A n'est pas unitaire, ben y'a plus de notion "d'inversible", ni dans A, ni, bien sûr, dans A[X] (donc pas de notion d'irréductible vu qu'on a besoin de la notion d'inversible pour définir les irréductibles). Bref, pour faire de "l'arithmétique", ça semble indispensable de supposer A unitaire.
- Si A n'est pas commutatif, alors on perd un des "théorème centraux" sur les polynômes, à savoir le fait que, si a est racine de P alors on peut factoriser X-a dans P. Et ça explique que, à un niveau élémentaire, on fait systématiquement l'hypothèse que A est commutatif lorsque l'on parle de A[X].
- Quelque soit A, on peut définir la notion de degré sur A[X], mais si A n'est pas intègre alors le degré d'un produit ne sera pas forcément égal à la somme des degrés (donc ça sert plus à grand chose...) et il est possible que des polynômes non constants soient inversibles (alors que si A est intègre, seuls les polynômes constants sont éventuellement inversibles).
- De plus, concernant justement les éléments inversibles de A[X], le cas où A est un corps est pas mal plus simple vu que dans ce cas, les inversibles de A[X] sont exactement les polynômes constants (non nuls).
- Mais ce qui, à mon avis, est la plus grande différence entre le cas où A est un corps et celui où il ne l'est pas, c'est que dans le cas d'un corps K, l'anneau K[X] est un anneau Euclidien (donc principal, donc factoriel) et qu'il y a des tonnes de théorèmes\définitions qui s'appliquent dans ce cas là, par exemple on est sûr que les pgcd existent et on sait même facilement les calculer avec l'algo. d'Euclide. Alors que , si A n'est pas un corps, ça se passe beaucoup moins bien. Par exemple on montre très facilement que Z[X] n'est pas un anneau principal donc surement pas Euclidien : adieu la division Euclidienne et tout ce qui va avec...

Par contre (et évidement), les définitions sont les mêmes (lorsqu'elles ont du sens dans le cas A quelconque évidement) : il n'y a que les théorèmes qui vont (pour certains d'entre eux) n'être valable que dans le cas Euclidien, donc dans le cas K[X] où K est un corps.

[Ncdk]

D'accord, c'est bien plus clair en effet.

C'est pour ça que dans les TD, systématiquement on demande si tel ou tel polynôme est irréductible dans Z[X] et ensuite de voir dans Q[X], car Q est un corps et Z est un anneau.
Autre chose, pour en revenir au tout début, dans ma définition, je voulais aussi bien comprendre, en appliquant la définition à Z[X] est-ce que la définition est équivalente à ça :

Soit P(X) non nul et non inversible de Z[X]. P(X) est irréductible signifie que P(X)=Q(X)R(X) implique que Q(X) ou R(X) = "+ ou -" 1

Du coup pour savoir si un polynôme est irréductible dans Z[X] on essaie de le factoriser quoi, si c'est possible alors directement il est réductible (Je pense pas que c'est le mot adéquat factorisable) et s'il ne l'est pas, alors il est irréductible. Je sais pas, ça me parait un peu trop facile du coup, je parle pour le degré 2 et moins bien sur.

Par contre dans Q[X] c'est un peu la même chose, sauf que les inversibles de Q c'est Q\{0}, donc toujours pareil, on regarde si on peut le factoriser par des polynômes non constants et puis on peut conclure.

Mais pour les degrés plus haut, style un polynôme de degrés 5, comment savoir s'il est irréductible ou pas dans Z[X] et Q[X] ?

[zygomatique]

ben on sort des théorèmes (ou toute sorte d'identités remarquables) de sa boite à outil qui permettent parfois de répondre à la question ...

ou on se débrouille on s'adapte ...

par exemple (très simple) est factorisable/réductible dans Z[x] donc dans Q[x] mais ne l'est pas dans Q[x] donc dans Z[x]

et en particulier en remplaçant la puissance 6 par 2 alors le premier a un discriminant qui est un carré parfait, ce qui n'est pas le cas du second ...

[Ncdk]

D'accord merci bien, après il doit y avoir certainement des techniques ou bien on est guidé dans l'exercice aussi

[Ben314]

Soit P(X) non nul et non inversible de Z[X]. P(X) est irréductible signifie que P(X)=Q(X)R(X) implique que Q(X) ou R(X) = "+ ou -" 1

Oui : vu que Z est commutatif, unitaire, intègre, les seuls polynômes inversible de Z[X] sont les polynômes constants égaux à un inversible de Z, donc à .

Ensuite, concernant l'irréductibilité, c'est effectivement très très simple... dans la théorie : si on ne peut pas factoriser, ben c'est irréductible.
Sauf que dans la pratique, ben c'est sacrément la m... : on a aucune caractérisation "immédiate" (style le déterminant d'une matrice pour savoir si elle est inversible ou pas) et on a par contre une multitude de "petits outils" qui s'appliquent dans certains cas particuliers. Bref, c'est exactement la même chose que, par exemple l'intégration : des tonnes de "petit trucs", mais rien qui "marche à tout les coups".

Par exemple, l'irréductibilité des polynômes cyclotomiques, ben c'est pas trop "trivial" comme truc....

[Ncdk]

Ah d'accord, bon c'est déjà plus clair dans ma tête, c'était ce qui me bloqué.

C'est vrai que du coup je me pose un tas de question sur l'irréductibilité, notamment avec les polynômes à coefficients dans Z/pZ, je me demande s'il est nécessaire de connaitre obligatoirement les inversibles de l'objet en question, parce-que les inversibles de Z/3Z, on les calcule pas, enfin je crois que je confond, mais bon autant dire ce que je pense. Dans les exercices avec Z/pZ on travaille souvent avec les classes des éléments dans Z/pZ est-ce par exemple prenons Z/3Z, on a 3 classes si je ne m'abuse, qui sont la classe de 0, celle de 1, et celle de 2.

Qu'est-ce que c'est ? Enfin je demande pas à ce qu'on me rappelle ce qu'est un anneau quotient, c'est juste me dire par exemple c'est quoi la classe de 1 dans Z/3Z, c'est tous les éléments de Z congru à 1 mod 3Z ?
Mais dans les exercices, il est fréquent qu'on manipule les classes, c'est surement bien plus rapide de travailler avec ça, plutôt que de s'embêter avec des congruences, mais c'est loin d'être évident pour moi.

Pour en revenir aux polynômes et les inversibles dans un anneau, comment on trouve par exemple les inversibles de Z/4Z, je prends cet exemple parce-que Z/2Z, Z/3Z ce sont des corps car 2 et 3 sont premiers, du coup si je dis pas de bêtises, pour Z/2Z, les inversibles sont la classe de 1 mais pas la classe de 0 ? Et pour Z/3Z c'est la classe de 1 et la classe de 2 mais pas la classe de 0 ?

C'est des choses qui sont trop flous pour moi, et du coup, quand j'ai un exercice avec du Z/pZ et des petites classes qui traînent, j'ai tout de suite peur, j'ai l'impression de rien savoir faire... Parce-que je ne comprends pas comment on travaille avec les classes, qui sont les inversibles tout ça tout ça (je sais même pas ce que ça fait d'additionner deux classes voir même de faire leur produit)

[Ben314]

De façon générale (et je suis à peu près sûr que tu l'a vu), les inversible de Z/nZ, c'est les classes des nombres premiers avec n.
Donc en particulier, si p est premier, tout élément autre que 0 de Z/pZ sont inversible : c'est un corps.
Sinon, tu as éventuellement aussi vu que le nombre d'élément inversible de Z/nZ, c'est phi(n) {indicatrice d'Euler} et que ça se calcule super facilement si on connait la décomposition en nombre premiers de n.

Sinon, concernant les congruences, il faut un jour ou l'autre "passer le cap" et comprendre que c'est quand même infiniment plus pratique d'écrire classe(a)=classe(b) avec une vraie égalité plutôt que a congru à b modulo...
Ne serait ce que pour avoir un ensemble de classe qu'on peut nommer (à savoir Z/nZ) et qu'on peut utiliser pour diverses construction (par exemple les polynômes à coeff. dans Z/nZ ou les fonctions de Z/nZ dans Z/mZ ou n'importe quoi du même style)
Et concernant les "opération basiques" (addition, multiplications, etc..) de toute façon, par définition même, c'est exactement la même chose qu'avec les congruence classe(a)+classe(b)=classe(a+b) et classe(a.b)=classe(a).classe(b) épicétou.
Le seul truc à comprendre, c'est que le + et le . à gauche des =, c'est des opérations sur les classes alors qu'à droite du =, c'est des opérations sur les entiers. Au début, on met parfois des rond autour du + et de . pour le différencier, puis rapidement on arrête vu que le contexte permet de savoir de quoi il s'agit.

[Ncdk]

D'accord, merci, c'est précis et clair, je vois tout de suite certains exercices déjà vu d'un autre œil.