Irrationnels

par **loulou231** » 04 Oct 2006, 11:08

Bonjour,
j'ai vraiment besoin d'aide pour cet exo, svp :

L'objectif est d'approcher racine de 2 d'aussi près que l'on veut par des nombres rationnels.

1) Montrer que si alpha est une valeur approchée par excès de racine de 2, 2/alpha est une valeur approchée par défaut. Montrer alors que, si alpha est compris entre 1 et 3, la moyenne arithmétique de ces deux valeurs approchées, c'est à dire 1/2(alpha +2/alpha), est un nombre supérieur à racine de 2 et qui est une meilleure valeur approchée de racine de 2 que alpha.

2) On considère alors la suite (Un) définie par U0 = 2 et Un+1 = 1/2(Un + 2/Un).

a) En utilisant un raisonnement par récurrence, montre que la suite (Un) est minorée par racine de 2 et étudier son sens de variation.

b) En déduire que la suite converge, puis que sa limite est racine de 2. La limite d'une suite de nombres rationnels est-elle nécessairement un nombre rationnel ?

Voilà le début de l'exo.
Merci d'avance
A+

par **Quidam** » 04 Oct 2006, 11:48

Facile pour un "supérieur" non ? Es-tu sûr qu'il fallait poster ça en "supérieur" ?

par **Imod** » 04 Oct 2006, 13:22

Il est vrai que l'exercice n'est pas difficile , je trouve en plus désolant qu'il soit vidé de sa signification géométrique ( ce qui en fait tout l'attrait ) .

Imod

par **loulou231** » 04 Oct 2006, 13:31

Bonjour, je sais que cet exo est simple pour le niveau"supérieur" mais c'est pour une amie qui est en TS.
Voilà, et moi j'ai un peu oublié ce genre de chose, c'est pour ça que je demandais de l'aide.

par **sandrine_guillerme** » 04 Oct 2006, 13:35

Salut,

J'espère que ceci pourra t'aider .

Bonne lecture :zen:

par **mathieu_t** » 04 Oct 2006, 13:47

Bon au risque de me faire lyncher, je donne des pistes (voire plus) pour la solution :

1) L'idée est d'utiliser la propriété

(tu peux vérifier ça facilement). Donc si d'un côté tu as

(avec alpha légèrement supérieur), c'est logique de trouver que

(avec 2/alpha légèrement inférieur).

2) (a) Tu dois voir le sens de variation, c'est à dire étudier le signe de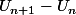

. Si tu regardes U1, U2, tu vois que ça décroit, donc par récurrence tu dois montrer que

(b) Il y a un théorème qui dit que toute suite décroissante et minorée converge. C'est le cas ici. Appelons cette limite

.
Quand n tend vers l'infini,

tend vers l, mais aussi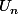

.
On peut donc écrire à la place de

l'égalité suivante :

.
Les solutions à cette équation sont

et

(le moins ne passe pas !).
Or la suite est minorée par

, donc sa limite ne pourra jamais être négative.
La seule limite est donc

.

En espérant que tu auras compris,

A+

par **sandrine_guillerme** » 04 Oct 2006, 14:04

La résolution des exercices est PROHIBEE !

La personne ne peut jamais avancer si tu gerbe la réponse de cette façon ..elle ne pourra jamais progresser et je ne crois pas que ça soit du tout gentille en faisant ça .. en tout cas c'est mon avis et c'est toi qui VOIT
A+

par **mathieu_t** » 04 Oct 2006, 14:31

Je n'ai pas l'impression d'avoir résolu l'ensemble des questions, juste donné les grandes lignes (bon ok un peu plus)... ensuite le dosage n'est pas facile !!

Ensuite je ne gerbe rien du tout, j'essaye juste d'aider !
Il y a aussi des fois où l'on a besoin de voir la solution pour comprendre le principe... C'est aussi comme cela que j'ai appris, certaines choses n'étant pas innées, et le fait de voir de nombreux exercices du genre nous donne les "trucs" pour le raisonnement...

Quant à savoir si je suis gentil ou pas de faire ça... Je ne sais pas... La plus belle solution est celle que l'on trouve soi-même (mais j'aurais tendance à plus appliquer ça au sens de ma vie plutôt qu'aux maths). Maintenant, sur un forum, les gens demandent de l'aide, c'est sans doute qu'ils n'ont pas trouvé eux-même...

par **Imod** » 04 Oct 2006, 14:37

Pour relativiser le problème vraiment récurrent sur ce forum comme sur d'autres , loulou231 pose la question pour aider une amie , laissons la faire la part de ce qu'elle doit délivrer à son amie de la solution de mathieu t .

Imod

par **sandrine_guillerme** » 04 Oct 2006, 17:50

mathieu_t a écrit:Je n'ai pas l'impression d'avoir résolu l'ensemble des questions, juste donné les grandes lignes (bon ok un peu plus)... ensuite le dosage n'est pas facile !!

Ensuite je ne gerbe rien du tout, j'essaye juste d'aider !
Il y a aussi des fois où l'on a besoin de voir la solution pour comprendre le principe... C'est aussi comme cela que j'ai appris, certaines choses n'étant pas innées, et le fait de voir de nombreux exercices du genre nous donne les "trucs" pour le raisonnement...

Quant à savoir si je suis gentil ou pas de faire ça... Je ne sais pas... La plus belle solution est celle que l'on trouve soi-même (mais j'aurais tendance à plus appliquer ça au sens de ma vie plutôt qu'aux maths). Maintenant, sur un forum, les gens demandent de l'aide, c'est sans doute qu'ils n'ont pas trouvé eux-même...

Ah nan pas du tout , il y a des gens qui disent que c'est un comptoir de Mc do Tu ecris l'exo et tu vien le récupérer le soir en racontant des barratins .. ca je connais ce forum avant d'y etre inscrit y a longtemps .. et c'est le cas généralement .. un peu moins au salon supérieur qu'au lycée et collège .. et je me suis fais des suggestions qu'en allant de cette base il y a ceux qui viennt au supérieur poster des question.. parceque ça serais relativement facile...
Bon brefons ..

A+

Irrationnels

irrationnels

Qui est en ligne