Bonsoir,
Je suis actuellement en train de faire mon dm, mais je bloque a quelques questions
L'énoncé est en pièce jointe car je n'arrive pas à insérer les équations avec Latex
J'en suis actuellement à la question 3)a),
J'ai essayé de développer w pour essayer de conclure quelque chose, mais je n'aboutis à rien
Auriez vous quelques conseils ?
Merci beaucoup
Irrationnalité de e
8 messages
- Page 1 sur 1
 Re: Irrationnalité de e
Re: Irrationnalité de e
Salut,
Pour les pièces jointes, il n'y a plus moyen de stocker quoi que ce soit directement sur le serveur du forum.
Donc il faut stocker sur un hébergeur autre puis mettre le lien ici.
Pour les pièces jointes, il n'y a plus moyen de stocker quoi que ce soit directement sur le serveur du forum.
Donc il faut stocker sur un hébergeur autre puis mettre le lien ici.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Irrationnalité de e
Ok, bon je vais taper le sujet comme ca
Soit n un entier naturel non nul
On pose Un = somme (k = 0 à n ) [1/k!]
Vn = Un + 1/(n * n!)
Tn = (1+1/n)^n
Wn = (1 - (1/n^2))^n
Apres avoir montré que Tn tends vers e et Wn tends vers 1, j'ai montré que
Tn = Somme (k = 0 à n) [ (1/k!) * produit (j = 1 à k) ((n-j+1)/n) ]
puis que pour n un entier naturel,
Tn <=Wn
Et maintenant, je dois montrer que :
Pour n un entier naturel, Vérifier que pour tout entier k entre 0 et n :
Wn <= Produit (j = 1 à k) [(n^3 - j + 1)/n]
et c'est ici que je suis bloqué
Voila, j'espère que la compréhension ne sera pas trop difficile, Merci par avance pour l'aide apportée
Soit n un entier naturel non nul
On pose Un = somme (k = 0 à n ) [1/k!]
Vn = Un + 1/(n * n!)
Tn = (1+1/n)^n
Wn = (1 - (1/n^2))^n
Apres avoir montré que Tn tends vers e et Wn tends vers 1, j'ai montré que
Tn = Somme (k = 0 à n) [ (1/k!) * produit (j = 1 à k) ((n-j+1)/n) ]
puis que pour n un entier naturel,
Tn <=Wn
Et maintenant, je dois montrer que :
Pour n un entier naturel, Vérifier que pour tout entier k entre 0 et n :
Wn <= Produit (j = 1 à k) [(n^3 - j + 1)/n]
et c'est ici que je suis bloqué
Voila, j'espère que la compréhension ne sera pas trop difficile, Merci par avance pour l'aide apportée
Re: Irrationnalité de e
Il y a des boulettes dans ton truc :
1) Ça peut pas être Tn <= Wn vu qu'on a trivialement Wn < 1 < Tn.
2) L'inégalité Wn <= Produit (j = 1 à k) [(n^3 - j + 1)/n] me semble franchement sans intérêt vu que Wn < 1 alors que le terme de droite est (beaucoup) plus grand que 1.
1) Ça peut pas être Tn <= Wn vu qu'on a trivialement Wn < 1 < Tn.
2) L'inégalité Wn <= Produit (j = 1 à k) [(n^3 - j + 1)/n] me semble franchement sans intérêt vu que Wn < 1 alors que le terme de droite est (beaucoup) plus grand que 1.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Irrationnalité de e
Oui effectivment, j'ai mal recopié.
J'ai montré que Tn <= Un (pas Wn)
Ensuite, je viens de me rendre compte de mon erreur, c'est un n^3 au dénominateur
Produit (j = 1 à n) [(1/n^3) * (n^3 - j +1) (qui lui n'est pas plus grand que 1)
Et c'est donc la que je bloque (Décidément j'ai fait beaucoup d'erreur de copie, encore désolé)
Merci pour les réponses
J'ai montré que Tn <= Un (pas Wn)
Ensuite, je viens de me rendre compte de mon erreur, c'est un n^3 au dénominateur
Produit (j = 1 à n) [(1/n^3) * (n^3 - j +1) (qui lui n'est pas plus grand que 1)
Et c'est donc la que je bloque (Décidément j'ai fait beaucoup d'erreur de copie, encore désolé)
Merci pour les réponses
Re: Irrationnalité de e
Si ce que tu doit montrer, c'est effectivement que ^{\!n}<\prod_{j=1}^n\dfrac{n^3-j+1}{n^3}) , ça résulte simplement du fait que
, ça résulte simplement du fait que 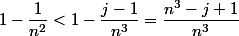 lorsque
lorsque  c'est à dire lorsque
c'est à dire lorsque  .
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Irrationnalité de e
Pour taper des formules Latex ; \dfrac{j-1}{n^3} , par exemple, et ensuite, tu sélectionnes la portion de texte en question, et tu cliques sur le bouton TEX
En fait, ce bouton ajoute simplement les balises Début-Tex et Fin-Tex autour du texte sélectionné.
Résultat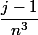
En fait, ce bouton ajoute simplement les balises Début-Tex et Fin-Tex autour du texte sélectionné.
Résultat
Re: Irrationnalité de e
@lycéen : tu as une idée de ce qu'il compte faire avec ce type de majoration sachant que le titre du fil c'est "irrationalité de e" ?
La méthode classique, ça utilise uniquement les suites (adjacentes) (Un) et (Vn).
Peut-être que c'est pour montrer que ces deux suites tendent vers e (en supposant que ce n'est pas connu du public à qui le D.M. est destiné) et en partant du fait, plus immédiat, que (Tn) tend vers e. Mais je ne vois pas à quoi peut servir cette majoration bizarre de Wn . . .
La méthode classique, ça utilise uniquement les suites (adjacentes) (Un) et (Vn).
Peut-être que c'est pour montrer que ces deux suites tendent vers e (en supposant que ce n'est pas connu du public à qui le D.M. est destiné) et en partant du fait, plus immédiat, que (Tn) tend vers e. Mais je ne vois pas à quoi peut servir cette majoration bizarre de Wn . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
