Bonjour,
Je suis en iut d'informatique, et le prof nous a démontré à l'arrache l'irrationnalité de racine de 2, mais je n'ai pas compris, car il a utilisé la méthode des valuations. Qu'est ce qu'une valuation ? A quoi est-ce que ça sert ? Quelles sont les valuations de 2 q² = p² ? Peut-on déduire d'une valuation si le nombre est pair ou impair ?
Irrationnalité de racine de 2
6 messages
- Page 1 sur 1
Armays a écrit:Bonjour,
Je suis en iut d'informatique, et le prof nous a démontré à l'arrache l'irrationnalité de racine de 2, mais je n'ai pas compris, car il a utilisé la méthode des valuations. Qu'est ce qu'une valuation ? A quoi est-ce que ça sert ? Quelles sont les valuations de 2 q² = p² ? Peut-on déduire d'une valuation si le nombre est pair ou impair ?
salut
si la racine carrée de 2 était un rationnel, on pourrait écrire:
Cela donne:
On pourrait écrire
Il y a une contradiction car
La racine carrée de 2 est irrationnelle.
chan79 a écrit:salut
si la racine carrée de 2 était un rationnel, on pourrait écrire:avec
et
entiers premiers entre eux
Cela donne:serait pair et donc
aussi.
On pourrait écrireet on aurait
serait pair et donc b aussi.
Il y a une contradiction caret
sont premiers entre eux.
La racine carrée de 2 est irrationnelle.
Oui j'ai compris cette méthode, mais je ne comprends pas la méthode des valuations.
Salut,
La "méthode des valuations" est très semblable à celle donnée par Chan, mais elle permet de se passer de l'hypothèse de départ "a et b premiers entre eux" (ce qui la rend légèrement plus technique)
Le seul truc à comprendre, c'est évidement la définition d'une "valuation" :
On montre alors facilement que=v_p(n)+v_p(m)) ce qui implique que
ce qui implique que =1+2v_2(b)) est forcément impair alors que
est forcément impair alors que =2v_2(a)) est forcément pair et donc on ne peut pas avoir
est forcément pair et donc on ne peut pas avoir 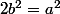 .
.
La "méthode des valuations" est très semblable à celle donnée par Chan, mais elle permet de se passer de l'hypothèse de départ "a et b premiers entre eux" (ce qui la rend légèrement plus technique)
Le seul truc à comprendre, c'est évidement la définition d'une "valuation" :
Définition a écrit:Siest un nombre premier et
un entier naturel non nul, on appelle valuation
-adique de
l'exposant de
dans la décomposition de
en nombres premiers (que l'on note
).
Exemples :donc
,
,
,
.
On montre alors facilement que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
La "méthode des valuations" est très semblable à celle donnée par Chan, mais elle permet de se passer de l'hypothèse de départ "a et b premiers entre eux" (ce qui la rend légèrement plus technique)
Le seul truc à comprendre, c'est évidement la définition d'une "valuation" :
On montre alors facilement quece qui implique que
est forcément impair alors que
est forcément pair et donc on ne peut pas avoir
.
Tu me fais (légèrement) penser à Grothendieck
Ben314 a écrit:Salut,
La "méthode des valuations" est très semblable à celle donnée par Chan, mais elle permet de se passer de l'hypothèse de départ "a et b premiers entre eux" (ce qui la rend légèrement plus technique)
Le seul truc à comprendre, c'est évidement la définition d'une "valuation" :
On montre alors facilement quece qui implique que
est forcément impair alors que
est forcément pair et donc on ne peut pas avoir
.
Salut Ben314, je ne comprends pas pourquoi :
v_p(n\times m)=v_p(n)+v_p(m)
v_2(2b^2)=1+2v_2(b)
v_2(2b^2)=1+2v_2(b) est forcément impair
v_2(a^2)=2v_2(a)
v_2(a^2)=2v_2(a) est forcément pair
Merci !
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
