Irrationalité d'une racine carrée

[pianiste06]

Bonjour,

Je vous soumets l'énoncé complet afin de comprendre l'intégralité du problème. J'ai trouvé les 2 premières questions et n'arrive pas à conclure sur la question 3. Je me permets de vous le soumettre; peut-être seriez vous plus éclairé que moi.

Merci par avance.
Voici l'énoncé

Soit a un entier strictement positif qui n'est pas le carré d'un autre entier. On se propose de démontrer que Racine(a) est irrationnel, c'est à dire que Racine(a) ne peut pas s'écrire sous la forme du quotient de deux entiers p et q avec q non nul. Pour cela nous allons raisonner par l'absurde.
Si a n'est pas le carré d'un entier, on peut l'encadrer par les carrés de deux entiers sucessifs, à savoir : n^2< a< (n+1)^2. Supposons alors que l'on puisse écrire
Racine(a) = p/q, la fraction ainsi écrite étant irréductible.
1) De Racine(a) = p/q et Racine(a) + n = (a - n^2)/(Racine(a) - n), déduire que p/q = (aq - np)/(p - nq).
2) Montrer que n 3) Conclure.

Laurent

[emdro]

Bonjour,

où en es-tu?

[yos]

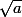
Bonsoir. Tu as une écriture de avec un dénominateur <q et c'est pas possible.

[emdro]

a la dernière apparemment.

Il faut que je me couche de plus en plus tôt, cela m'inquiète!

Désolé!

[pianiste06]

C'est justement ce qu'il faut démontrer... l'incohérence. Mais je ne vois pas trop comment conclure.
Je sais qu'il s'agit d'un raisonnement par l'absurde; mais je sens que je passe à côté de la conclusion.

[emdro]

Comme t'a dit Yos, tu as réussi dans la question précédente à trouver une fraction égale à p/q de dénominateur inférieur à q, alors que p/q était irréductible.

[pianiste06]

Ca, c'est vraiment intelligent.

Mille mercis à vous.

[emdro]

Merci à toi: je ne connaissais pas cette démonstration! :id: