Bonjour,
Une fois de plus, je ne suis pas certain d'aborder un sujet touchant le lycée ou le supérieur. Merci de réorienter le message si erreur il y a.
Je n'ai pas de question précise. J'ai lu, relu et rerelu l'information relative au fameux Mu de Moebius. Je comprends ce que l'on cherche, mais j'applique avec 1001 bourdes. je vais élaborer un exemple inventé et fort simple (supposément! ). J'aimerais que vous m'aidiez à le terminer.
(E (d/n)= Sommation des diviseurs de n )
Disons F(n) = 1/n
1/n = E(d/n) f(d) .... une fois manipulée --> f(n) = E(d/n) Mu(d) F(n/d)
Donc
f(n) = E (d/n) Mu(d) d/n
f(n) = 1/n E (d/n) Mu(d)d
Rendu là ... je sais que je dois utiliser la forme canonique pour ''biffer'' certains trucs. Je pourrai également faire ''sauter'' mon E (d/Qi^ai) Mu (d) ..... mais je fais des erreurs dans la manipulation probablement puisque je n'arrive à rien.
En plus, je n'ai pas trouvé (pas cherché) comment écrire avec le symbolisme mathématique sur le forum et cela devient lourd à transcrire.
Merci de m'ouvrir les yeux, les matheux
Max, right from Québec.
L'inversion de Moebius pour les nuls
8 messages
- Page 1 sur 1
par Ben314 » 12 Nov 2010, 22:02
Salut,
1) Pour "les formules mathématiques", c'est bien expliqué là : http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
Sinon, tu peut aussi "citer" (par exemple ce post) pour voir (et copier) comment on tape des formules
2) Assez clairement, ce type de question, dans la nomenclature française, c'est du "supérieur" : le lycée, ça s'arrête vers 18 ans.
3) Concernant ton problème, pour le moment, tout me semble parfaitement correct et effectivement, il y a peut être moyen de simplifier=\frac{1}{n}\Bigsum_{d|n}\mu(d)d)
, mais comme ça fait longtemps que je n'ai pas manipulé, je vois pas trop quoi faire de mieux...
1) Pour "les formules mathématiques", c'est bien expliqué là : http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
Sinon, tu peut aussi "citer" (par exemple ce post) pour voir (et copier) comment on tape des formules
2) Assez clairement, ce type de question, dans la nomenclature française, c'est du "supérieur" : le lycée, ça s'arrête vers 18 ans.
3) Concernant ton problème, pour le moment, tout me semble parfaitement correct et effectivement, il y a peut être moyen de simplifier
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par MaxQuébec » 12 Nov 2010, 22:17
D'ack merci pour le tuyau.
Pour le problème offert. Je viens de tomber sur un exemple tel quel avec F(n) = 1/n
 = 1/{p^a} \bigsum_{d|p^a} d MU(d) = (1/(p^a)) ( 1 - p ))
Par ailleurs, Et cette conclusion? Elle a un lien avec la transformation de la sommation .... le changement du Mu par 1 ou -1 je crois ... mais j'y vois pas clair.
Je vous dis si j,allume
D'ici là, :0
Max
Pour le problème offert. Je viens de tomber sur un exemple tel quel avec F(n) = 1/n
Par ailleurs, Et cette conclusion? Elle a un lien avec la transformation de la sommation .... le changement du Mu par 1 ou -1 je crois ... mais j'y vois pas clair.
Je vous dis si j,allume
D'ici là, :0
Max
par Ben314 » 12 Nov 2010, 22:43
Bon, d'abbord, pour le Latex, il y a encore de petits progrés à faire... :zen:
Sinon, pour = \frac{1}{p^a} \bigsum_{d|p^a} d \mu (d))
, c'est vite plié : les diviseurs de 
sont 
(si 
) et leur "mu" respectifs sont 
d'où...
Ne pas perdre de vue la définition de la fonction
:
Si
avec les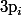 
distincts et les 
alors =\left\{\matrix{ (-1)^n&{\rm si tout les }\lambda_i\ {\rm vallent }1\cr 0&{\rm si un des }\lambda_i\ {\rm est }\geq 2\ \ \ \ }\right.)
Sinon, pour
Ne pas perdre de vue la définition de la fonction
Si
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par MaxQuébec » 12 Nov 2010, 22:56
J'étais revenu sur le forum justement pour dire que je venais de comprendre! (DÉsolé pour l'écriture mathématique 
)
Merci du tuyau.
Ce genre de problème se résolve ainsi. Qu'en est-il des questions de la forme '' Soit
, et  = \bigsum_{d|n} TO(d))
, trouver une formule pour F(n) en fonction de la représentation canonique de n.
J'ai la réponse, mais je me bloque rapidement. (C'est un exercice pour pratiquer... ca pratique ma patience)
)Merci du tuyau.
Ce genre de problème se résolve ainsi. Qu'en est-il des questions de la forme '' Soit
J'ai la réponse, mais je me bloque rapidement. (C'est un exercice pour pratiquer... ca pratique ma patience)
par Ben314 » 12 Nov 2010, 23:48
Ok, c'est ce que l'on apelle "l'indicatrice d'Euler". Trés souvent, on la note 
.
Concernant ta somme, effectivement, ça se simplifie pas mal :=n)
Il y a des tas de façons de le démontrer...
La plus jolie est sans doute de voir que dans un groupe cyclique d'ordre n, pour tout d divisant n, il y a exactement)
éléments d'ordre d. Comme tout élément du groupe possède un ordre, lorsque l'on ajoute tout les , on obtient le nombre total d'éléments du groupe, c'est à dire n.
On doit pouvoir aussi le faire "à la main" en utilisant le fait que, si
alors =(p_1-1)p_1^{\alpha_1-1} (p-2-1)p_2^{\alpha_2-1}...(p_k-1}p_k^{\alpha_k-1})
lorsque les 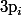sont distincts et les 
mais ça risque d'être un peu lourd à écrire...
Concernant ta somme, effectivement, ça se simplifie pas mal :
Il y a des tas de façons de le démontrer...
La plus jolie est sans doute de voir que dans un groupe cyclique d'ordre n, pour tout d divisant n, il y a exactement
On doit pouvoir aussi le faire "à la main" en utilisant le fait que, si
mais ça risque d'être un peu lourd à écrire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par MaxQuébec » 12 Nov 2010, 23:57
TO c'est le nombre de nombres premiers avec n, plus petits que n.
par Ben314 » 13 Nov 2010, 00:24
Ok, c'est ce que l'on apelle "l'indicatrice d'Euler". Trés souvent, on la note .
Concernant ta somme, effectivement, ça se simplifie pas mal :
Il y a des tas de façons de le démontrer...
La plus jolie est sans doute de voir que dans un groupe cyclique d'ordre n, pour tout d divisant n, il y a exactement éléments d'ordre d. Comme tout élément du groupe possède un ordre, lorsque l'on ajoute tout les , on obtient le nombre total d'éléments du groupe, c'est à dire n.
On doit pouvoir aussi le faire "à la main" en utilisant le fait que, si alors lorsque les 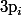sont distincts et les
mais ça risque d'être un peu lourd à écrire...
Concernant ta somme, effectivement, ça se simplifie pas mal :
Il y a des tas de façons de le démontrer...
La plus jolie est sans doute de voir que dans un groupe cyclique d'ordre n, pour tout d divisant n, il y a exactement
On doit pouvoir aussi le faire "à la main" en utilisant le fait que, si
mais ça risque d'être un peu lourd à écrire...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :