Inversion matrice symétrique creuse
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mathelot
 par mathelot » 03 Mai 2008, 16:19
par mathelot » 03 Mai 2008, 16:19
bjr,
je cherche à inverser la matrice:

avec une diagonale de 4 et deux sous-diagonales de 1.
merçi d'avance.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Mai 2008, 17:41
par leon1789 » 03 Mai 2008, 17:41
Quel est son polynôme caractéristique (remplacer les 4 par 4-T) ?
-
mathelot
 par mathelot » 03 Mai 2008, 18:12
par mathelot » 03 Mai 2008, 18:12
Ils vérifient la relation de récurrence
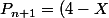P_{n}+P_{n-1})

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 03 Mai 2008, 18:34
par leon1789 » 03 Mai 2008, 18:34
mathelot a écrit:Ils vérifient la relation de récurrence
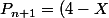P_{n}+P_{n-1})
J'aurais dit

, non ?
Pour simplifier les calculs, il vaut mieux poser T = 4-X .
On peut probablement calculer son polynôme caractéristique (en T) en défaisant la formule récurrente ?
(une remarque : le polynôme caractéristique en T est de même parité que n :happy2: )
-
mathelot
 par mathelot » 03 Mai 2008, 18:37
par mathelot » 03 Mai 2008, 18:37
je souhaite surtout inverser cette matrice. j'ai essayé la méthode LU
mais je ne m'en suis pas sorti.
-
jeanphi
- Messages: 1
- Enregistré le: 03 Mai 2008, 17:42
-
 par jeanphi » 03 Mai 2008, 18:56
par jeanphi » 03 Mai 2008, 18:56
Salut,
pour mon premier post, j'ai peur de dire une bêtise, mais bon je me lance.
Il me semble qu'on peut se ramener à inverser une matrice de la forme Id - M, avec M matrice avec deux sous-diagonales de -1/4.
Comme M^n tend vers la matrice nulle, l'inverse de Id-M est la somme géométrique des M^k, et on peut donc en déduire l'inverse de 4(Id-M).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités