Inverse d'une matrice, quand existe-t-elle ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
azerty21
- Messages: 7
- Enregistré le: 28 Fév 2010, 20:34
-
 par azerty21 » 03 Mar 2010, 17:48
par azerty21 » 03 Mar 2010, 17:48
Bonjours,
Je code un programme sur Maple et j'ai besoin j'obtenir l'inverse d'une matrice, mais l'obtient un message d'erreur car elle n'est pas inversible.
Je me suis documenté sur l'inversion des matrices mais je ne comprend toujours pas.
Alors comment peut-on savoir concrètement lorsque une matrice est inversible ?
Merci.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 17:51
par Nightmare » 03 Mar 2010, 17:51
Salut,
Il y a plusieurs méthodes. La plus "élémentaire" consiste à montrer que son noyau est réduit au seul vecteur nul, en résolvant le système associé à la matrice. Une autre consiste à calculer son déterminant et montrer qu'il n'est non nul. Et bien d'autres encore...
-
azerty21
- Messages: 7
- Enregistré le: 28 Fév 2010, 20:34
-
 par azerty21 » 03 Mar 2010, 19:18
par azerty21 » 03 Mar 2010, 19:18
Ok, merci.
Mais petite précision, une matrice symétrique n'admet pas d'inverse ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 19:19
par Nightmare » 03 Mar 2010, 19:19
Pourquoi pas?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 03 Mar 2010, 19:19
par girdav » 03 Mar 2010, 19:19
Si, l'identité est une matrice symétrique qui admet un inverse.
-
azerty21
- Messages: 7
- Enregistré le: 28 Fév 2010, 20:34
-
 par azerty21 » 03 Mar 2010, 19:50
par azerty21 » 03 Mar 2010, 19:50
En faite je fait un programme qui integre l'algorithme de Levenberg-Marquardt
Je doit calculer:
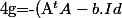^{-1}A^tj)
Mais dans tous les cas possible le déterminant de

est toujours nuls et donc la matrice n'est pas inversible.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Mar 2010, 19:54
par Nightmare » 03 Mar 2010, 19:54
Sauf que ce n'est pas AtA qu'on veut inverser !
-
azerty21
- Messages: 7
- Enregistré le: 28 Fév 2010, 20:34
-
 par azerty21 » 03 Mar 2010, 20:09
par azerty21 » 03 Mar 2010, 20:09
Ok, c'est sur que si j'inverse la mauvaise matrice je vais pas m'en sortir !
Un grands merci à toi Nightmare.
-
gigamesh
- Membre Rationnel
- Messages: 712
- Enregistré le: 26 Fév 2010, 03:32
-
 par gigamesh » 03 Mar 2010, 21:07
par gigamesh » 03 Mar 2010, 21:07
det(AtA) = det(A) * det(tA) = det(A)*det(A) !
Donc A inversible <=> AtA inversible
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
