Inverse d'une application

[Pikachue]

Bonjour,

Je cherche l'inverse de l'application qui à une matrice B symétrique définie positive associe AB+BA où A est une matrice symétrique définie positive fixée.
J'ai essayé plusieurs choses, mais ça ne marche jamais... J'ai l'impression que ce n'est pas si compliqué pourtant!

Pourriez-vous m'aider, s'il vous plaît?

[Robot]

Tu peux commencer par considérer le cas où A est la matrice identité, puis voir s'il n'y a pas moyen de s'y ramener ...

[Pikachue]

C'est ce que j'essaye de faire. Si A=In alors l'inverse de la fonction qui à B donne (1/2)B.
Mais pour s'y ramener, je n'y arrive pas, puisque rien ne commute, donc par exemple si j'envoie B sur A*B (Où je note A* l'inverse de A pour simplifier les notations) ou sur BA*, j'arrive à simplifier un côté de la somme mais pas l'autre.
J'ai essayé d'envoyer B sur des sommes du style A*B+BA* en espérant que tout se simplifie mais ça ne marche pas non plus...

[Robot]

Normalement, tu devrais savoir qu'il existe une matrice orthogonale telle que .

Edit : [B]Là, j'ai écrit une grosse bêtise. Désolé ![/B]

[Pikachue]

Je croyais qu'il existait P orthogonale telle que PAP^-1 est diagonale, par la symétrie de A, mais avec comme éléments diagonaux les valeurs propres de A (pas forcément égales à 1, mais strictement positives puisque A est définie positive)...

Donc non, je ne connaissais pas l'existence de P orthogonale comme vous la décrivez...
Quel argument nous donne son existence?

[Robot]

Au temps pour moi, tu as raison !
Ce que je voulais dire, c'est qu'il existe une matrice inversible telle que .

[Pikachue]

Mais la matrice P dont je parle dans ma réponse précédente est orthogonale, c'est-à-dire que son inverse est égale à sa transposée, n'est-ce pas? Donc mon message précédent soulève la même interrogation que ce soit pour (transposée de P)AP=In ou (p^-1)AP=In :lol2:
Je ne sais pas si je me fais comprendre!

[MouLou]

Non, la matrice ici n'est pas orthogonale, juste inversible!

[Pikachue]

J'ai pourtant sous les yeux un résultat énoncé dans un livre disant "Soit M dans Mn(R) symétrique. Alors il existe C une matrice orthogonale telle que (C^-1)MC=D où D est diagonale"...

[mathelot]

on peut avoir le titre et le nom de l'auteur ? merci.

[MouLou]

Oui, a ne pas confondre avec, "toute matrice symétrique définie positive est congruente à la matrice identité".

[Pikachue]

L'auteur est Xavier Gourdon.
D'accord, donc si on a en plus que la matrice M est définie positive, on a (transposée de C)MC =In pour une certaine matrice C inversible?

[Pikachue]

Ah, au temps pour moi, j'ai trouvé la propriété dont vous parlez dans le livre! Je ne la connaissais pas du tout!
Je vais essayer de l'utiliser pour trouver l'inverse de ma fonction, et je vous dirai quoi!

Merci pour vos indications.

[Pikachue]

Je n'ai pas réussi... J'ai noté R (et transp(R) sa transposée) la matrice telle que R.A.transp(R)=In (avec les notations de A et B précédentes).
J'ai essentiellement utilisé le fait que R.A=transp(R)^-1 et que A.transp(R)=R^-1 pour essayer de trouver l'inverse, en envoyant par exemple B sur R.B.transp(R). J'ai essayé aussi d'utiliser le fait que B est symétrique, qui implique que transp(B)=B, pour passer de transp(R).B à transp(B.R), mais je crois que ça ne sert à rien en fait.
Est-ce ce genre de choses que je suis censée faire, ou est-ce que je ne suis pas du tout sur la bonne voie?

[Matt_01]

Pour moi, c'est la propriété que tu utilises qui peut être utile (à savoir que tu peux diagonaliser dans une base orthonormale). Tu peux traiter le cas A diagonale et ensuite généraliser.

[Robot]

Une réponse bricolée qui ne me satisfait pas vraiment. (Mais elle est complète).
1°) Supposons diagonale, de coefficients diagonaux .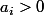
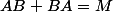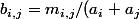Etant donné , pour trouver l'unique tel que , prendre ( 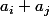n'est jamais nul).
2°) Pour symétrique définie positive quelconque, il existe orthogonale telle que soit diagonale à coefficient diagonaux .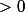
Appliquer alors la méthode précédente à .

Remarque : la matrice peut être quelconque.

[Pikachue]

Mais pourquoi pourrait-on appliquer la première méthode dans la deuxième?
(DP^-1) n'est pas forcément diagonale, si? Et même si c'était le cas, on a des termes des deux côtés de B, donc pourquoi pourrait-on appliquer ce qui précède?

[Robot]

Mais est diagonale à coefficients positifs ! Et si on connaît , on connaît , n'est-ce pas ?
Là je t'ai donné vraiment beaucoup d'indications, tu devrais pouvoir y arriver.