Intersection d'une droite et d'un cercle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MrKnightley
- Membre Naturel
- Messages: 10
- Enregistré le: 09 Fév 2019, 18:46
-
 par MrKnightley » 09 Fév 2019, 19:05
par MrKnightley » 09 Fév 2019, 19:05
Bonjour tout le monde,
Voici l'énoncé d'un exercice que j'essaie de résoudre :
1) Soit Q=(-1, 0). Fixons t un réel et notons T=(0, t). Déterminer l'équation cartésienne de la droite (Dt) qui passe par Q et T.
J'ai procédé ainsi :
(Dt) :
y = mx + pLes coordonnées de Q vérifient
0 = -m + p, donc
p = m.
Les coordonnées de T vérifient
t = p, donc
p = m = t.
(Dt) a donc pour équation y = tx + t 2) Montrer que (Dt) intersecte le cercle unité C en deux points : Q et P, dont on déterminera les coordonnées (x, y).
Le cercle unité a pour équation x² + y² = 1, donc je résous le système :
• x² + y² = 1
• y = tx + t
Ce qui me donne :
x² + (tx +t)² = 1
x² + t²x² + 2t²x + t² - 1 = 0
x² + x(t²x + 2t²) + t² - 1 = 0Et là je bloque... Je ne sais pas comment m'en sortir avec toutes ces variables. Le calcul du discriminant
Δ est trop compliqué pour que j'arrive à en tirer quelque chose d'utile.
Quelqu'un aurait-il une solution ? Merci d'avance !
-
aviateur
 par aviateur » 09 Fév 2019, 19:23
par aviateur » 09 Fév 2019, 19:23
Bonjour
Il serait bien d'écrire ton équation sous la forme


n'est pas compliqué mais de toute on peut s'en passer. En effet x=-1 est racine évidente.
Pour avoir l'autre racine tu peux utiliser la somme des 2 racines qui vaut -b/a ou le produit qui vaut c/a
.
-
MrKnightley
- Membre Naturel
- Messages: 10
- Enregistré le: 09 Fév 2019, 18:46
-
 par MrKnightley » 09 Fév 2019, 19:44
par MrKnightley » 09 Fév 2019, 19:44
Merci, Aviateur. J'ai l'équation :
x² + x(t²x + 2t²) + t² - 1 = 0 avec :
a = 1
b = (t²x + 2t²)
c= t² - 1
Effectivement, les relations entre les racines sont bien pratiques.
Donc X1 * X2 = c/a
..................... X2 = - c/a = -t² + 1
En remplaçant X2 dans l'équation de la droite : (Dt) : y = tx + t
On trouve y = t(-t² + 1) + t
......................y = -t^3 + 2t
Parfait, je te remercie.
Modifié en dernier par
MrKnightley le 09 Fév 2019, 19:55, modifié 2 fois.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 09 Fév 2019, 19:54
par Lostounet » 09 Fév 2019, 19:54
MrKnightley a écrit:Merci, Aviateur. J'ai l'équation :
x² + x(t²x + 2t²) + t² - 1 = 0 avec :
a = 1
b = (t²x + 2t²)
c= t² - 1
Effectivement, les relations entre les racines sont bien pratiques.
Donc X1 * X2 = c/a
..................... X2 = - c/a = -t² + 1
En remplaçant X2 dans l'équation de la droite : (Dt) : y = tx + t
On trouve y = t(-t² + 1) + t
......................y = -t^3 + 2t
Parfait, je te remercie.
Pas si vite !
Comment ça se fait que b dépend de x ?!
Le coefficient devant x^2 ne devrait pas être 1 mais (1+t^2)....
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
MrKnightley
- Membre Naturel
- Messages: 10
- Enregistré le: 09 Fév 2019, 18:46
-
 par MrKnightley » 09 Fév 2019, 20:23
par MrKnightley » 09 Fév 2019, 20:23
Ah, oui je n'ai pas factorisé les bons éléments. Je trouve donc :
(1 + t²)x² + (2t²)x + t² - 1 = 0
X1 * X2 = c/a
..........X2 = - c/a
..........X2 = - (t²-1) / (t² + 1)
Je pourrais factoriser X2 en - (t - 1)(t+1) / (t + i)(t- i) en utilisant les complexes, mais je ne vois pas trop comment simplifier ça...

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Fév 2019, 20:35
par chan79 » 09 Fév 2019, 20:35
salut
x²+(tx+t)²=1
Pour x=-1, l'équation est vérifiée (solution évidente si on la voit...)
ensuite x²-1+t²(x+1)²=0
-
aviateur
 par aviateur » 09 Fév 2019, 21:10
par aviateur » 09 Fév 2019, 21:10
Bonjour
Q=(-1,0) est sur le cercle, c'est pour ça que -1 est racine évidente.
Ensuite l'autre racine est bien
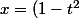/(1+t^2),)
il n'y pas vraiment plus simple.
Alors y=t+xt donne pour x=-1 y=0 (on retrouve Q)
et pour x=(1-t^2)/(1+t^2) on trouve y=(2 t)/(1 + t^2)

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 09 Fév 2019, 21:56
par Lostounet » 09 Fév 2019, 21:56
Sinon le calcul de delta n'est pas si difficile... pas
Indispensable de faire appel à des racines évidentes ou des astuces...
(1 + t²)x² + (2t²)x + t² - 1 = 0
Delta = 4t^4 - 4(1+t^2)(t^2-1)
= 4t^4 - 4[ t^2 - 1 + t^4- t^2]
= 4
x1=(-2t^2 - 2)/(2(1+t^2)) = -1
x2= (-2t^2+2)/(2(1+t^2))= (-t^2+1)/(1+t^2)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 09 Fév 2019, 23:19
par chan79 » 09 Fév 2019, 23:19
Lostounet a écrit: pas Indispensable de faire appel à des racines évidentes ou des astuces...
(1 + t²)x² + (2t²)x + t² - 1 = 0
Salut
Je suis d'accord; la méthode normale est de passer par le calcul de

.
Sinon, on a une interprétation géométrique.

La droite Dt a comme ordonnée à l'origine t et comme pente t . Elle passe par C et A et recoupe le cercle en B.
Les coordonnées de B sont
, sin(\theta)))
t=tan(

/2) (angle inscrit égal à la moitié de l'angle au centre)
D'après les formules du demi angle:
les coordonnées de B sont:
)
-
MrKnightley
- Membre Naturel
- Messages: 10
- Enregistré le: 09 Fév 2019, 18:46
-
 par MrKnightley » 10 Fév 2019, 12:21
par MrKnightley » 10 Fév 2019, 12:21
Ah, oui, je n'étais pas arrivé à simplifier Δ, mais on tombe bien sur un entier au final. Merci beaucoup pour votre aide, je vais m'attaquer à la suite !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités

