Intersection de plans

[PythagoreSauvage]

J'ai l'exercice suivant :

Déterminer où P1 est le plan engendré par les vecteurs (1, 1, 0) et (2, 1, 1) et P2 est le plan engendré par les vecteurs (1, -1, 0) et (2, 1, -1)

J'ai essayé de caractériser l'intersection de ces deux plans en employant le vecteur normal :

Soit un vecteur normal à . Il est à la fois normal à P1 et P2 donc vérifie :






On aboutit alors au système suivant :



mais je ne sais pas trop quoi en faire, j'ai l'impression qu'il manque une donnée dans l'exercice, la donnée d'un point par exemple ?

[lyceen95]

Quand j'étais lycéen, on parlait de plans (ou plans affines quand on veut pinailler) et par ailleurs de plans vectoriels. Un plan affine, c'est par exemple le plan d'équation z=1, ou z=2. Ces 2 plans sont parallèles.

Un plan vectoriel, c'était une 'direction'. Ces 2 plans sont associés au même plan vectoriel (ils sont parallèles, ils ont même direction). Le plan vectoriel en question est engendré par exemple par les vecteurs (1,0,0) et (0,1,0).

Il y a une infinité de plan affines portés par un plan vectoriel unique. Ils sont tous parallèles entre eux. Tous les plans horizontaux dans le cas de mon exemple.

Ca, c'était avant.

Maintenant, si j'ai tout suivi, ce qu'on appelle plan, c'est un plan vectoriel, et non un plan affine ; c'est donc une 'orientation'.

L'intersection de 2 plans ... Un plan affine qui croise un plan affine, c'est une droite affine. Effectivement définie par un point et une orientation.
Un plan vectoriel qui croise un autre plan vectoriel, c'est une droite vectorielle, une direction.
Ce qu'on cherche, c'est un VECTEUR. C'est le vecteur qui donne la direction de cette droite.

Si tu veux te ramener à des plans affines, tu peux choisir un point ((0,0,0) par exemple), utiliser les plans affines qui passent par ce point, et engendrés par les vecteurs de l'exercice. Chercher la droite affine intersection de ces plans affines. Et chercher le vecteur directeur de cette droite.

Pour les calculs, je n'ai pas l'impression que passer par un vecteur normal à P1 et P2 soit la bonne piste.

[GaBuZoMeu]

Bonjour,
Par contre ce qui peut se faire, c'est de trouver un vecteur normal à , un vecteur normal à , puis un vecteur normal au plan engendré par et . Ce vecteur est donc à la fois dans et ...
Trouver un vecteur normal à un plan engendré par deux vecteurs, rien de plus simple si on connaît le produit vectoriel.

[PythagoreSauvage]

Oui je me doutais que c'était cette distinction entre plan au sens affine ou vectoriel qui posait problème et je suis assez d'accord, autant fixer le point A(0;0;0). De là on peut déjà obtenir les équations cartésiennes de P1 et P2.

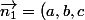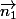
Pour ça, on trouve le vecteur normal à P1. Soit on utilise immédiatement le produit vectoriel, et on obtient que soit on écrit que doit vérifier et

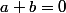
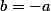
Ainsi on a et . En exprimant tout en fonction de a, il vient et . Ainsi (1,-1,-1) convient.

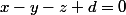
L'équation cartésienne de P1 est donc : et en prenant A(0;0;0) on trouve d = 0

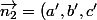De même on trouve une équation cartésienne du plan P2. Soit un vecteur normal à P2. On a . Une équation cartésienne de P2 est

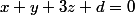
Alors l'intersection de P1 et P2 vérifie les équations suivantes :




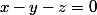
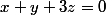
En additionnant on a 2x = -2z soit x = -z et par suite y = -2z. Ainsi est la droite dirigée par le vecteur (-1,-2,1)

[GaBuZoMeu]

Je ne vois pas pourquoi faire intervenir cette histoire de plan affine. On est clairement ici en algèbre linéaire, on travaille avec des sous-espaces vectoriels de .

[PythagoreSauvage]

J'ai compris où vous vouliez en venir effectivement, et c'est encore plus rapide

qui on le remarque est colinéaire au vecteur trouvé avec la "méthode" affine