Intersection ellipse et droite

[Oliegus]

Bonjour,

Dans le cadre d'un projet informatique, mon équipe et moi-même travaillons sur un programme graphique en java.

Une des étapes est la suivante: Pouvoir supprimer des objets dans une zones défini par un clic de souris. Cet objet peut être une ellipse.

Pour savoir si la zone de suppression se trouve à l'intérieur de l'ellipse. Nous aurions besoin de savoir comment calculer les points d'intersection d'une droite et d'une ellipse.

Nous avons effectué beaucoup de recherche sur ce thème... sans succès. :triste:

Pour une droite y=ax+b et une ellipse de centre quelconque dans un plan 2D. On connait les différentes caractéristiques de l'ellipse. (Largeur,hauteur)

En espérant avoir une réponse,

Merci.

[Cheche]

Salut,

Si tu connais la valeur de la largeur et de la hauteur :

alors l'équation de l'ellipse est :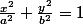

Avec a et b les paramètres de l'ellipse (tu devrais les trouver avec "la largeur et de la hauteur", vocabulaire qui n'existe pas pour une ellipse).


Enfin, pour trouver les intersections, une résolution de système par informatique devrait suffire.

[uztop]

Bonjour,

l'equation que tu donnes est l'equation reduite, qui n'est valable que si l'ellipse est centree sur l'origine et ses axes sont paralleles aux axes du repere.
Pour une zone de selection, je suppose que les axes sont bien paralleles aux axes du repere mais il faut trouver les coordonnes du centre de l'ellipse (= centre du rectangle de selection) et l'equation devient

[Oliegus]

Merci pour ces réponses.

Et surtout pour le complément de uztop.

Vraiment efficace votre forum.

Bye