Intersection cône/cylindre

[gilsub]

Bonjour,
Dans le cadre d'un projet en informatique, j'ai besoin de récupérer l'équation paramétrique du "cercle déformé" intersectant un cône et un cylindre de révolution. Je possède les équations paramétriques du cône et du cylindre, qui sont :
- Cylindre
x=r*cos(theta)
y=r*sin(theta)
z=h
où theta et h sont les deux paramètres, r=1.

-Cône
x=heigth+0.6
y=((hc-heigth)/hc)*rc*sin(theta)
z=((hc-heigth)/hc)*rc*cos(theta)+heigth/1.2+0.6
où heigth et theta son les deux paramètres, hc la hauteur du cône et rc son diamètre.

La représentation graphique ressemble à un arrosoir.
Si je ne me trompe pas, la méthode serait de passer en équations cartésiennes et de résoudre l'une égale à l'autre.

D'après http://mathworld.wolfram.com/Cone.html, si je transforme l'équation de mon cône cela donnerai :
(z^2+y^2)/((rc/hc)^2)=(x-hc)^2
En prenant l'équation du cylindre : x^2+y^2=r^2 , j'ai donc essayé de résoudre ce système, sans succès, je tourne en rond et n'aboutis à rien.

Ma question est donc : serait-il possible d'avoir une piste de départ pour le résoudre?
Merci d'avance de vos conseils.

[Ben314]

Salut,
Bon, déjà, entre les équations paramétriques de ton cône et son équations cartésiennes, ça déconne : il est clair que si on remplace x,y et z par leurs valeurs dans l'équation cartésienne, ça marche pas => Laquelle des deux correspond à ton problème ?

De plus, tes équations paramétriques ne sont pas celle d'un cône "de révolution" (le sommet n'est pas à la verticale du centre du cercle formant la base) est-ce voulu ?

[gilsub]

Salut et merci de ta réponse :)
Celle qui correspond à mon problème est
x=heigth+0.6
y=((hc-heigth)/hc)*rc*sin(theta)
z=((hc-heigth)/hc)*rc*cos(theta)+heigth/1.2+0.6

Effectivement ce n'est pas un cône de révolution...mon but est d'avoir une figure ressemblant à un arrosoir car c'est la forme que j'étudie en ce moment, mais à la limite ce n'est pas réellement un problème (donc oui c'est voulu). Ce qui m'intéresse c'est la méthode qui me permettrai de trouver l'équation du "cercle" intersectant les deux formes car je vais devoir le refaire pour beaucoup d'autre cas.

Dans le cas ou je n'ai aucune idée de la forme de l'équation cartésienne du cône, comment puis-je passer de la forme paramétrique à la forme cartésienne?

[nuage]

Salut,
En utilisant l'équation du cylindre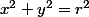 il est assez facile de déterminer en fonction de heigth.
Ce qui donne x, y et z en fonction de heigth. C'est à dire une équation paramétrique de la courbe d'intersection.

Elle n'est pas très élégante, il faut faire attention aux signes de sin(theta) et cos(theta) et au domaine de variation de height, mais en principe ça marche.

[Ben314]

En général, lorsque tu cherche l'intersection de deux "objets" (sous espaces vectoriels, surfaces de R³, courbes de R²,...) l'idéal est de connaitre une (des) équation(s) paramétrique(s) de l'un et une (des) équation(s) cartésienne(s) de l'autre.
Ici, au départ, tout est en paramétrique => c'est la merde.
Mais, ton cylindre a clairement pour équation cartésienne x²+y²=r². Tu n'as plus qu'à remplacer x et y par les valeurs donner par les équations paramétriques du "cône" pour trouver à quelle condition sur 'height' et sur le 'theta' (du cône) un point du cône est aussi sur le cylindre.

Edit : trés forte redite de mon message avec celui de Nuage (j'ai commencé à tapé, puis fait autre chose puis...)

[gilsub]

Bonjour, et merci de vos réponses.

Procédant selon vos conseil, j'ai donc obtenu :
sin²(theta)=[r^2-(height+0.6)^2]/[((hc-height)/hc)*rc]^2
J'en déduis cos²(theta) = 1-sin²(theta) , puis j'enlève les carrés en mettant une racine de l'autre côté, et enfin je remplace dans l'équation paramétrique du cône. J'obtiens bien en effet x, y, et z en fonction de height uniquement. Seulement quand je trace ça avec matlab, j'obtiens une droite appartenant au cône...
J'ai vérifier plusieurs fois la façon dont j'ai rentré les équations, cela ne vient pas de là.
Est-ce que je me suis trompé quelque part?