Intersection de boules fermées dans R^n

[suno]

EN triant de vieux papiers, dont mes cours, exercices et questions de concours d'entrée divers, je suis tombé sur un pb que je ne sais plus résoudre (ainsi que d'autres, mais je me souviens bien de celui-ci qui m'a valu une très bonne note à un oral - preuve que je l'avais résolue). Aujourd'hui loin des maths de taupe... je ne sais plus faire.

En simplifiant l'énoncé : étant donnée une famille finie de boules fermées de R^n, qui ont la propriété suivante: l'intersection de 3 boules quelconques de la famille est non vide, prouver l'intersection des boules de la famille est non vide.

Convexité + R^N, mais je n'ai pas trouvé.

Merci d'avance
S.

PS: c'est évidement généralisable à une famille quelconque via un argument de compacité.

[GaBuZoMeu]

Bonjour,

L'énoncé tel que tu l'as transcrit est faux : place 4 boules fermées identiques avec leurs centres aux sommets d'un tétraèdre régulier de côté 1 et leur rayon plus grand que et plus petit que .

[suno]

Bonjour,

L'énoncé est celui que je donne, il n'a pas à être faux ou juste, c'est une donnée ! La réponse que tu donnes est visiblement une solution d'un autre problème, en dimension 3.

Merci de relire mon énoncé - dimension quelconque >=1, famille finie de taille quelconque etc.

Merci néanmoins.

[GaBuZoMeu]

Relis mieux ma réponse.
L'énoncé que tu as simplifié demande de démontrer un résultat qui est faux. Je t'ai donné un contre-exemple.

[Ben314]

Salut,
A la limite, on peut signaler que le Théorème de Helly dit que, en dimension quelconque, si l'intersection de boules quelconques de l'ensemble est toujours non vide alors l'intersection globale sera non vide.
Donc si c'est les intersection de 3 boules qui est systématiquement non vide, alors l'intersection globale est non vide . . . à condition d'être en dimension 2.

[suno]

L'énoncé que tu as simplifié demande de démontrer un résultat qui est faux. Je t'ai donné un contre-exemple.

Voilà ce qu'il manquait à ta réponse pour que je puisse la comprendre... Mais je maintiens que mon énoncé n'est pas faux : il énonce une proposition fausse.

[GaBuZoMeu]

L'énoncé "Si une famille finie de boules fermées de a la propriété que l'intersection de 3 boules quelconques de la famille est non vide, alors l'intersection des boules de la famille est non vide." est faux.
Ça te va comme ça ?
Vois-tu pourquoi je t'ai bien donné un contre-exemple ?

[suno]

L'énoncé "Si une famille finie de boules fermées de a la propriété que l'intersection de 3 boules quelconques de la famille est non vide, alors l'intersection des boules de la famille est non vide." est faux.
Ça te va comme ça ?
Vois-tu pourquoi je t'ai bien donné un contre-exemple ?

Oui, ça me va. Et j'ai ma réponse avec le théorème de Helly. Donc je suppose que l'énoncé dont je me souvenais pas très bien était en dimension 3 et qu'il s'agissait d'intersections de 4 boules quelconques.

Merci à tou(te)s

[GaBuZoMeu]

Ou dans le plan et avec l'intersection de 3 disques quelconques. Ce n'est déjà pas évident.
Dans la droite avec l'intersection de deux intervalles quelconques, c'est plus reposant.

[suno]

Ce qui m'étonne réstrospectivement, c'est que j'avais trouvé rapidement (dim 3, inter 4 à 4, seulement des boules, pas des convexes quelconques), donc il doit y avoir une démonstration élémentaire.

[Ben314]

De mémoire (et je peut rechercher si besoin...), il y a au moins une preuve élémentaire du théorème de Helly en commençant par démontrer ce que j'ai toujours appelé le "théorème de Carathéodory" et qui n'est pas exactement le même que celui de Wiki (à voir si ce n'est pas la même chose énoncé différemment ou alors... je me goure de nom pour le théorème...) :
Si on prend un ensemble de points d'un espace affine de dimension , alors on peut scinder l'ensemble en deux parties (non vides) telles que l'intersection des deux enveloppes convexes des deux parties soit non vide.
Exemple : En dimension 3, si on a 5 points alors soit un des 5 est à l'intérieur du tétraèdre formé par les 4 autres, soit il y a deux points qui sont les extrémités d'un segment qui perce le triangle de sommets les 3 autres. (et s'il n'y a pas 4 points coplanaires parmi les 5, c'est un seul des 5 + 10 = 15 cas de figure qui est vérifié)

[Ben314]

Théorème : (qui, pour moi s'appelle "de Carathéodory", mais peut-être me fourvoie-je...)
Si est une famille de points d'un espace affine de dimension alors il existe une partition de en deux sous familles non vides et telle que les enveloppes convexes de et de soient sécantes.

Preuve :
Si , comme la famille de vecteurs est forcément liée donc il existe des réels non tous nuls tels que .

Si on fixe un et qu'on pose on a donc .
Si on prend alors et on peut écrire que où tout les coefficients sont positifs et où ce qui signifie que le barycentre de est le même que celui de .

[GaBuZoMeu]

Je fais pour le plan, avec des disques.
On a une famille finie de disques fermés tels que trois quelconques d'entre eux aient toujours une intersection non vide. On veut montrer que l'intersection de la famille est non vide.
On peut supposer sans perte de généralité que : (*) aucun disque ne contient l'intersection de deux autres dans son intérieur (sinon, on enlève ce disque de la famille). On choisit un disque D dont le cercle frontière C a un point P qui n'appartient pas à la réunion des autres disques. Les autres disques tracent sur C privé de P (une droite, n'est-ce pas ?)) une famille finie d'intervalles fermés dont les intersections deux à deux sont toujours non vides grâce à (*) ; cette famille finie d'intervalles a donc une intersection non vide, et un point de cette intersection est dans l'intersection de tous les disques de la famille de départ.
Exercice : copier pour une famille de boules dans l'espace de dimension 3.

[Ben314]

La preuve que je connaissait :
Théorème de Helly:
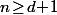
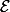
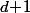
Si on a une famille de convexes d'un espace affine de dimension telle que toute intersection de convexes de la famille soit non vide alors l'intersection des convexes de la famille est non vide.

Preuve :
On procède par récurrence sur .
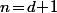
Pour , il n'y a rien à démontrer.
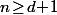
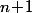
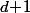
On suppose donc le résultat vrai pour un entier donné et on se donne une famille de convexes telle que l'intersection de quelconques d'entre eux soit non vide.
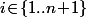
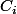
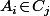
Par hypothèse de récurrence, pour tout , l'intersection de tout les convexes sauf est non vide donc il existe un point tel que pour tout .
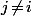
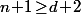
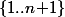
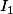
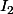
Comme la famille contient points, on peut appliquer le théorème précédent qui nous dit qu'on peut partitionner en deux parties non vides et de façon à ce que l'enveloppe convexe de et celle de aient au moins un point commun .
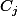
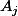
Or, si on prend un des convexes de la famille, il contient tout les points sauf au plus un (à savoir le point ) donc il contient tout les points d'une des deux familles ou bien et, comme il est convexe, il contient l'enveloppe convexe de la famille en question et, dans les deux cas, il contient en particulier le point .