Interpolation Polynomiale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
wacho
- Messages: 3
- Enregistré le: 04 Avr 2007, 19:44
-
par wacho » 04 Avr 2007, 20:49
Bonjour à tous
, j'aimerai avoir quelques indications pour l'exercice suivant:
On considère la suite de fonction
=cos(n.Arccos(x)))
, x compris entre [-1;1]
(a) démontrer que l'on a la relation
=2xP_n(x)-P_{n-1}(x))
(b) En déduire que Pn(x) est un polynome de degré n
Pour le (a), j'ai essayé de faire un changement de variable pour avoir la forme cos(nx) et utiliser les polynomes de Tchebychev mais je m'en sors pas vraiment^^ Pourriez-vous m'orienter sans me donner les réponses toutes faites.
Merci à vous
-
mathelot
par mathelot » 04 Avr 2007, 20:56
Il y a la formule qui donne le cosinus de la somme de deux arcs:
=\cos(a)\cos(b)-\sin(a)\sin(b))
et le raisonnement par récurrence:
)
et
 \Right P(n+1)) \Right (\forall n P(n)))
-
wacho
- Messages: 3
- Enregistré le: 04 Avr 2007, 19:44
-
par wacho » 04 Avr 2007, 22:14
Merci beaucoup mathelot; voila le calcul que j'ai effectué :
cela revient à demontrer, je vais apeler Arccos x : A pour un souci de lisibilité^^
 + P_{n-1}(x)=2xP_n(x))
 + P_{n-1}(x)= cos((n+1).A) + cos ((n-1).A))
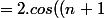.A + (n+1).A). cos ((n-1).A - (n-1).A))
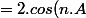. x)
cqfd
Pour la b, en réécrivant
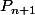
, j'en arrive à :
) - \sqrt{1-x^2}.sin(n.Arccos (x)))
et la je bloque un peu^^ serais-je parti dans un délire astral :p
Encore merci pour le temps que vous passerai à me porter secours
-
mathelot
par mathelot » 05 Avr 2007, 08:24
Pour la (b), on calcule les deux expressions
)
et
)
et ensuite, de proche en proche, par une récurrence,
on prouve que
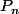
est une fonction polynomiale, en effet les fonctions polynomiales forment une algèbre.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
par fahr451 » 05 Avr 2007, 09:39
wacho a écrit:Pour le (a), j'ai essayé de faire un changement de variable pour avoir la forme cos(nx) et utiliser les polynomes de Tchebychev mais je m'en sors pas vraiment^^ Pourriez-vous m'orienter sans me donner les réponses toutes faites.
Merci à vous
bonjour juste une remarque
les Pn sont exactement les polynômes de tchebychev
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
par