je n arrive pas du tout a faire cette exercice pouvez vous m aider
1)pout tout k de {1,...,n} montrer qu'il existe un unique polynome L_k tel
deg(Lk)<=n-1 Lk(Xk)=1 et pour toutj appartenant à {1,...,n}/{k},Lk(Xj)=0
on donnera l expression factoriseé du polynome Lk
2)Montrer que pour tout P de R_n-1[X], on a P=sum(P(Xk)*Lk,k=1..n)
3)pour tout k de {1...n on pose lk=int(Lk(t)dt de 0 a 1)
P est un element de R_2n-1[X] on sair que l on a l egalite int(P(t)dt de 0 a 1) =sum(lk*P(xk),k=1..n)
prouver que pour tout j de {1...n} lj>0 en posant P=Lj^2
je n arrive absolument pas a avancer sauf pour la question a
merci d avance.
PS bonne annee
Interpolation polynomiale
9 messages
- Page 1 sur 1
Le polynome P prend les valeurs
,P(x_{2}) \cdots P(x_{n}}) aux points
aux points 
Le polynome*L_{j}) est de degré au plus n-1 et prend la valeur
est de degré au plus n-1 et prend la valeur ) en
en 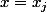 et 0 sur les (n-1) autres valeurs
et 0 sur les (n-1) autres valeurs 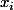 .
.
tu remarques que dans cette expression, est un polynome tandis que
est un polynome tandis que ) est un nombre.
est un nombre.
d'où les polynomes P et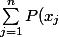L_{j}) prennent
prennent
les mêmes valeurs en n points. comme ils sont de degré au plus n-1, ils sont égaux.
Le polynome
tu remarques que dans cette expression,
d'où les polynomes P et
les mêmes valeurs en n points. comme ils sont de degré au plus n-1, ils sont égaux.
interpolation polynomiale
il y a une question precedente ou on dit:
Un=X^n*(X-1)^n/n! et Pn est la derive n eme de Un
pour tout k de {1...n on pose lk=int(Lk(t)dt de 0 a 1)
P est un element de R_2n-1[X].prouver que
int(P(t)dt de 0 a 1) =sum(lk*P(xk),k=1..n)
je sais que je dois utiliser la division de p par Pn,P=QPn+R avec deg(Q)
.Cela est donner comme indication
merci
Un=X^n*(X-1)^n/n! et Pn est la derive n eme de Un
pour tout k de {1...n on pose lk=int(Lk(t)dt de 0 a 1)
P est un element de R_2n-1[X].prouver que
int(P(t)dt de 0 a 1) =sum(lk*P(xk),k=1..n)
je sais que je dois utiliser la division de p par Pn,P=QPn+R avec deg(Q)
.Cela est donner comme indication
merci
il y a encore une autre question sur laquelle je bloque
on reprend les notations des questions precedentes
on considere l approximation int(f(t)dt, de0 à1)=sum(lkf(Xk,k=1..n) ou f:[0,1]-> R est continue
on sait que l approximation est en fait une egalite si f est un polynome de degres<=2n-1
on cherche a etudier la qualite de cette approximation quand f est de classe C2n
4) montrerqu il existe un unique P appartenant a R_2n-1[X] tel ke pour tout k appartenant a {1.....n} P(Xk)=f(Xk) et P'(Xk)=f'(Xk)
je sais ke je dois poser P=QPn+R avec Q,R dans Rn-1[X] et utiliser la question2 mais je n y arrive pas
merci d avance
on reprend les notations des questions precedentes
on considere l approximation int(f(t)dt, de0 à1)=sum(lkf(Xk,k=1..n) ou f:[0,1]-> R est continue
on sait que l approximation est en fait une egalite si f est un polynome de degres<=2n-1
on cherche a etudier la qualite de cette approximation quand f est de classe C2n
4) montrerqu il existe un unique P appartenant a R_2n-1[X] tel ke pour tout k appartenant a {1.....n} P(Xk)=f(Xk) et P'(Xk)=f'(Xk)
je sais ke je dois poser P=QPn+R avec Q,R dans Rn-1[X] et utiliser la question2 mais je n y arrive pas
merci d avance
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
