Interpolation polynomiale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 31 Mar 2014, 08:56
par Ben314 » 31 Mar 2014, 08:56
Salut,
Le polynôme
}{b_j(x_j)})
est
l'unique polynôme de degré
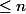
valant 0 sur tout les

sauf sur
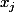
où il vaut 1.
Et celui de l'autre coté du "égal", il est de degrés combien ?
Il vaut combien en
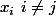
? et en
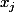
?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
sorabreath
- Messages: 6
- Enregistré le: 31 Mar 2014, 08:26
-
 par sorabreath » 31 Mar 2014, 11:03
par sorabreath » 31 Mar 2014, 11:03
Ben314 a écrit:Salut,
Le polynôme
}{b_j(x_j)})
est
l'unique polynôme de degré
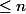
valant 0 sur tout les

sauf sur
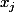
où il vaut 1.
Et celui de l'autre coté du "égal", il est de degrés combien ?
Il vaut combien en
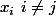
? et en
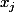
?
A droite le degrés est < ou = à n-j qui est plus petit que n.
en x_i il vaut ? je ne sais pas comment trouver c'est vraiment pas très clair pour moi la forme bj(x) j'ai beau retourné mon cours dans tout les sens.
En tout cas merci pour la réponse si rapide!
Du coup on se fait aider sur le forum et on aide ceux qu'on peut aider ? sympa comme principe.
-
sorabreath
- Messages: 6
- Enregistré le: 31 Mar 2014, 08:26
-
 par sorabreath » 31 Mar 2014, 18:43
par sorabreath » 31 Mar 2014, 18:43
Je suis vraiment coincé je demande pas une solution mais vraiment un coup de pouce j'ai limpression de ramer et c'est pire après 8H de travail ... merci le temps plein.
-
sorabreath
- Messages: 6
- Enregistré le: 31 Mar 2014, 08:26
-
 par sorabreath » 01 Avr 2014, 22:11
par sorabreath » 01 Avr 2014, 22:11
Personne pour un petit coup de main en plus ? :s
merci.

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 02 Avr 2014, 04:53
par alm » 02 Avr 2014, 04:53
Salut
Pour tout
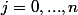
, posons
=\frac{b_j(x)}{b_j(x_j)})
1) Que vaut le degré de
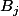
? ( tu peux remarquer que c'est un produit de

monômes de degré

chacun)
2) Que vaut
)
?
3) Que vaut
)
pour
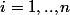
et
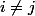
Posons maintenant
=\frac{b_{n-j}(-x)}{b_{n-j}(x_{n-j})})
Tu va démontrer que
1) degré
)
=degré
)

2)pour tout
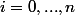
on a
=C_j(x_i))
(pour cela discute deux cas : 1er
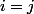
2em
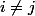
.)
Tu conclut par unicité du polynôme interpolateurde Lagrange

tel que
=0)
si
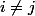
et
=1)
.
-
sorabreath
- Messages: 6
- Enregistré le: 31 Mar 2014, 08:26
-
 par sorabreath » 02 Avr 2014, 07:16
par sorabreath » 02 Avr 2014, 07:16
Merci beaucoup c'est clair et parfait !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
est l'unique polynôme de degré
valant 0 sur tout les
sauf sur
où il vaut 1.
? et en
?