Intérieur polygone convexe

[maikeer]

Bonjour,

Soit un polygone convexe dans un environement 2D. Je recherche la formule qui permet de determiner, à partir des sommets du polygone, la position d'un point à l'intérieur ou à l'éxtérieur de ce polygone.

Je vous remercie par avance pour votre aide.

Maikeer.

[Blueberry]

Bonjour, disposes-tu

1) d'une liste des sommets a0,a1,...,an telle que chaque aiai+1 et ana0 soit un côté du polygone ?

2) d'un point appartenant à l'intérieur du polygone ?

[maikeer]

Je dispose de la liste des sommets du polygone. Je souhaite savoir si le point (x,y) est à l'intérieur du polygone convexe.

Merci d'avance.

[nuage]

Salut,
On a les sommets du polygone dans l'ordre (ie est un côté du polygone convexe.
Le point M est à l'intérieur du polygone ssi M est du même côté de la droite que le point quelque soit i, tout ça modulo n.
Or le point M est du même côté de la droite AB que le point C ssi le déterminant de et à le même signe que le déteminant de et .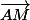

Il suffit donc de regarder le signe du déterminant de et car le déterminant de et a un signe constant.

Mes excuses, je suis un peu las.
Tu peux me redemander explications et justifications.

A+