Intégrer p fois fraction rationnelle simple

[Wenneguen]

Bonjour,

comment s'y prendre pour intégrer p fois par rapport à x : ?

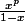
Merci ! :we:

[Nightmare]

Salut,

tout d'abord, arrives-tu à primitiver une première fois? Si oui qu'obtiens-tu?

[Wenneguen]

Salut,

tout d'abord, arrives-tu à primitiver une première fois? Si oui qu'obtiens-tu?

Non je n'y arrive pas :briques:

[Nightmare]

Essaye dans un premier temps de décomposer en éléments simples

[jlb]

Non je n'y arrive pas :briques:

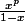
le doit te rappeler l'expression de la somme des termes d'une suite géométrique... à peu de chose près!!

[Wenneguen]

Essaye dans un premier temps de décomposer en éléments simples

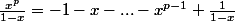
Ok, et donc en intégrant une première fois ça donne

[Wenneguen]

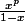
le doit te rappeler l'expression de la somme des termes d'une suite géométrique... à peu de chose près!!

Oui c'est comme ça que j'ai obtenu cette expression justement :lol2:

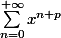
D'ailleurs, c'est peut-être mieux d'intégrer cette expression sous la forme ? ( mon but et d'exprimer la p-ième primitive de cette expression " à l'aide des fonctions usuelles ", c'est à dire sans somme j'imagine )

[jlb]

Oui c'est comme ça que j'ai obtenu cette expression justement :lol2:

continue d'intégrer l'expression, le terme génant c'est log|1-x| mais en pensant aux primitives de log, une petite adaptation astucieuse va faire l'affaire

[Wenneguen]

continue d'intégrer l'expression, le terme génant c'est log|1-x| mais en pensant aux primitives de log, une petite adaptation astucieuse va faire l'affaire

Tu pourrais m'en dire plus sur cette adaptation astucieuse ? ^^

[jlb]

Tu pourrais m'en dire plus sur cette adaptation astucieuse ? ^^

-(1-x)ln(1-x) -x doit convenir [ tu intègres par partie avec -(1-x) pour primitive de 1 dans 1*ln(1-x)] comme primitive de ln(1-x) et tu poursuis en intégrant par partie( dérivation de ln(1-x) et intégration de (1-x)^k) pour avoir l'intégrale souhaitée.