Intégrer des vecteurs

par **Zweig** » 08 Juil 2009, 16:37

Salut,

Je suis tombé sur ça dans le livre d'Hecht :

http://yfrog.com/2jhecht2p

La première intégrale intègre des vecteurs et dont les bornes sont des vecteurs (membre de gauche) ! Je dois dire que ça dépasse mon imagination ... Une explication s'impose :we:

Merci !

par **Skrilax** » 08 Juil 2009, 16:42

(juste une petite précision pour les autres : dans ce livre, les vecteurs sont notés en gras)

Moi aussi j'aimerais bien savoir :we:

par **Zweig** » 08 Juil 2009, 16:43

Plus généralement, c'est une "convention" chez les anglais en Physique de mettre les vecteurs en gras.

par **Dominique Lefebvre** » 08 Juil 2009, 16:46

Zweig a écrit:Plus généralement, c'est une "convention" chez les anglais en Physique de mettre les vecteurs en gras.

c'est une convention chez tous les physiciens, comme j'ai eu l'occasion de le dire souvent ici....

par **Zweig** » 08 Juil 2009, 16:48

Ah d'accord, il me semblait que tu m'avais dit à l'époque que c'était une spécificité des anglais :marteau: ...

par **Dominique Lefebvre** » 08 Juil 2009, 17:04

Zweig a écrit:Ah d'accord, il me semblait que tu m'avais dit à l'époque que c'était une spécificité des anglais :marteau: ...

Initialement oui (il y a 50 ou 60 ans..) mais depuis une vingtaine d'années, voire plus, tous ont adoptés cette convention, qui simplifie grandement l'écriture!

Pour en revenir au problème que tu poses, l'intégration de fonctions vectorielles n'a rien de surprenant. Il existe un tas de formules célèbres et à connaitre qui intégrent des fonctions vectorielles (Green, Otsro, Riemann, Stokes, etc.).
On ramène pour le calcul la fonction vectorielle (ou tensorielle d'ailleurs) à ses composantes.
Ce qui est plus inusité dans Hecht, c'est l'utilisation de bornes vectorielles, ici des impulsions p. Ce n'est pas très orthodoxe, mais c'est légitime, dans la mesure où l'élement différentiel (le dp) est lui-même vectoriel.

par **Zavonen** » 08 Juil 2009, 17:28

Dominique Lefebvre a écrit: Ce n'est pas très orthodoxe, mais c'est légitime, dans la mesure où l'élement différentiel (le dp) est lui-même vectoriel.

Pas très orthodoxe, c'est sûr! Légitime j'en doute.
Je ne vois que deux cas où cette écriture peut avoir un sens.
a et b étant les bornes vectorielles
1) Raccourci pour exprimer la différence F(b)-F(a) où F est une fonction définie sur un ensemble de vecteurs et dont dérive la forme que l'on intègre. Je ne vois pas trop l'intérêt de cette notation m'enfin ...
2) Il s'agit de l'intégrale sur un circuit allant de a à b et on est dans le cas où l'intégrale ne dépend pas du chemin emprunté (par exemple pour les fonctions analytiques).
A part ces deux exemples, je ne vois vraiment pas à quoi correspond cette notation.

par **skilveg** » 08 Juil 2009, 17:31

Bonsoir,

Dominique Lefebvre a écrit:Ce n'est pas très orthodoxe, mais c'est légitime

C'est légitime dans le sens où c'est une convention "à la physicienne" pour désigner ce qui n'est rien d'autre qu'une intégrale sur un segment (réel): on intègre de

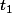à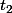

, instants auxquels la quantité considérée vaut

et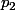

[pardon si j'ai changé les notations]. Hors contexte, ça n'a pas de sens: on ne sait pas comment

et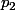

sont reliés.

Pour en rajouter dans le rigorisme mathématique, mettre des bornes dans une intégrale n'a formellement de sens que si on intègre sur un segment de

; sinon, on ne peut pas faire mieux que préciser la partie mesurable sur laquelle on intègre.

[Post écrit en même temps que Zavonen, pour dire à peu près la même chose ^^]

par **Dominique Lefebvre** » 08 Juil 2009, 17:34

Zavonen a écrit:Pas très orthodoxe, c'est sûr! Légitime j'en doute.

Si, si, pour le commun des mortels physiciens, c'est légitime. On va dire qu'au moins c'est très parlant! J'ai vu des auteurs employer des écritures bien plus olés!
C'est un raccourci commun mais que personnellement je n'emploie pas, car il déroute le lecteur néophyte. Alors dans un bouquin de cours de ce niveau, c'est moyen, je te le concède...

par **Zavonen** » 08 Juil 2009, 17:45

Si, si, pour le commun des mortels physiciens, c'est légitime. On va dire qu'au moins c'est très parlant! J'ai vu des auteurs employer des écritures bien plus olés!

Très vieux débat, entre les 'gardiens du temple' et les 'utilisateurs' justifiant l'existence du temple par les besoins qu'ils ont créés.
On va conclure. Il faut de tout pour faire un monde scientifique des mathématiciens ET des physiciens.

Intégrer des vecteurs

Intégrer des vecteurs

Qui est en ligne