Intégration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 13 Oct 2009, 14:33
Bonjour,
Soit f une fonction continue sur [0,1] et g une fonction continue sur R et périodique de période 1. Montrer que, quand n tends vers l'infini,
g(nx)dx)
tends vers
dx)*(\int_{0}^{1}g(x)dx))
Je ne vois pas vraiment par où commencer...
Je remarque qu'intégrer entre 0 et 1 g(nx) revient à intégrer entre 0 et n g(x)...
Merci !
par busard_des_roseaux » 13 Oct 2009, 14:45
on peut chercher parallèlement !
voilà deux tuyaux classiques:
i) l'espace des polynomes est dense dans celui des fonctions continues
définies sur [0,1]. on peut supposer f et/ou g polynôme
ii) l'espace des fonctions C1 est aussi dense dans c0.
on peut supposer f et g continuement dérivables
iii) concernant le produit des deux intégrales, on peut rentrer l'une dans l'autre
(linéarité) ! et ensuite effectuer la soustraction
ps: source d'inspiration : la continuité du produit de convolution
iv) et il y a les séries de Fourier, g étant 1-périodique. mais là, il faut C1 par morceaux, il me semble qu'il y a des fonctions continues qui ne sont pas somme de leur série de Fourier, même pas au sens des moyennes de Césaro.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 13 Oct 2009, 15:49
Salut !
Un truc qui peut être intéressant :
En posant
on a alors :
h(nx)dx=\Bigint_{0}^{1}f(x)g(nx)dx-\(\Bigint_{0}^{1} f\)\(\Bigint_{0}^{1} g\))
Il suffit donc de montrer que la propriété est vraie pour une fonction continue 1-périodique d'intégrale nulle sur sa période !
par busard_des_roseaux » 13 Oct 2009, 16:18
deux autres pistes:
i)
ce que l'on appelle la deuxième formule de la
moyenne te permet de "sortir" f(x) de l'intégrale
 g(nx)dx)
la 1ère formule de la moyenne aussi.
par busard_des_roseaux » 13 Oct 2009, 17:04
autre démo (la 1ère n'étant pas finalisée)il y a de la bilinéarité ! en effet c'est le produit (réel)
de deux formes linéaires.
il est possible qu'il suffise de vérifier la formule sur les intégrales du type
dx)
et
dx)
puis le résultat final par densité et bilinéarité à gauche des polynomes (Weiertrass) et à droite des polynomes trigonométriques.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 13 Oct 2009, 17:23
En utilisant une de tes idées combinée à la mienne busard_des_roseaux :
g(nx)dx\le ||f||_{\infty} \Bigint_{0}^{1} g(nx)dx)
En posant
dx=\frac{1}{n}\Bigint_{0}^{n} g(x)dx=\Bigint_{0}^{1} g(x)dx=0)
La propriété est vraie pour g d'intégrale nulle sur [0,1] CQFD
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
par jeje56 » 14 Oct 2009, 06:19
Nightmare a écrit:Salut !
Un truc qui peut être intéressant :
En posant
on a alors :
Il suffit donc de montrer que la propriété est vraie pour une fonction continue 1-périodique d'intégrale nulle sur sa période !
Salut Nightmare,
La dernière intégrale, c'est pas 1/n fois l'intégrale entre 0 et n de g plutôt ?
Edit : c'est la même chose... Autant pour moi !
Merci !
par busard_des_roseaux » 14 Oct 2009, 07:18
Nightmare a écrit:
comment on obtient ça ? (g n'est pas nécéssairement de signe constant)
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
par Doraki » 14 Oct 2009, 08:04
1. Montrer que si f est constante c'est vrai.
2. Approcher f par des fonctions constantes par morceaux.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 14 Oct 2009, 10:53
Oula oui je me suis emporté sur ma démo, surtout que je suppose g d'intégrale nulle sur [0,1] difficile alors d'y être de signe constant !
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 14 Oct 2009, 14:59
Soit
cette intégrale. Divisons l'intervalle
en
parties égales suffisament petites pour que
)
y soit de signe constant, et écrivons que
g(nx)dx)
D'après la formule de la moyenne, sur chaque intervalle
il existe
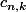
tel que l'on peut écrire
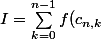\int_{\frac kn}^{\frac{k+1}n}g(nx)dx)
Dans cette dernière intégrale, posons
soit
ce qui donne
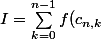\frac 1n\int_ k^{k+1}g(u)du)
Comme
)
est périodique de période 1,
du=\int_0^1g(u)du)
, quant à
)
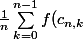sa limite est par définition
dx)
D'où la relation ...
-
mathelot
par mathelot » 14 Oct 2009, 15:09
Pythales a écrit:Soit
cette intégrale. Divisons l'intervalle
en
parties égales suffisament petites pour que
)
y soit de signe constant
=x sin(\frac{1}{x}))
?
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
par isortoq » 15 Oct 2009, 06:26
Bonjour !
Si f est de classe C1, on peut intégrer par parties...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
