Intégration

[Kimou]

Soit un espace mesuré tel que soit - fini. On munit de la tribu Borélienne et on considère une fonction mesurable

Un moment donné il faut calculer:


Et d'après la correction s'est égal à:
( )
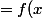Questions:
Comment passer de la première égalité à la deuxième?
autre question j'arrive pas a comprendre le "1" dans et enfin le fait que l'intégral se rapporte à la variable "t" ici, il faut lire l'indicatrice en fonction juste de t?
Oui j'ai un peu de mal avec tout ça..
Merci d'avance !

[Kimou]

Personne ?

[girdav]

La fonction à intégrer vaut si et sinon. Comme est positive on a juste à intégrer lorsque est compris entre et .

[Kimou]

La fonction à intégrer vaut si et sinon. Comme est positive on a juste à intégrer lorsque est compris entre et .

D'accord merci, et le "1" dans il signifie quoi concrètement?

[girdav]

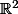
C'est la mesure de Lebesgue sur (comme je pense que ton problème vient de l'intégration sur , ça permet d'éviter une confusion).

[Kimou]

Ok.. autre petite question tant que j'y suis.
Enoncé:
Pour on pose:
G(x)=
Montrer que
Correction:
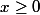
pour et 1 intégrable sur [0,1]. On veut en fait appliquer le théorème de convergence dominée, mais pourquoi dit on que 1 est intégrable sur cet intervalle plutôt que sur [0,2]? D'où ca sort?

[Kimou]

Ok.. autre petite question tant que j'y suis.
Enoncé:
Pour on pose:
G(x)=
Montrer que
Correction:
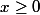
pour et 1 intégrable sur [0,1]. On veut en fait appliquer le théorème de convergence dominée, mais pourquoi dit on que 1 est intégrable sur cet intervalle plutôt que sur [0,2]? D'où ca sort?

[girdav]

En fait je ne comprends pas pourquoi on applique le théorème de la convergence dominée, puisque l'on peut écrire que .

[Kimou]

En fait je ne comprends pas pourquoi on applique le théorème de la convergence dominée, puisque l'on peut écrire que .

Oui tu as parfaitement raison, il le met en remarque qu'une simple majoration suffit, mais vu qu'on était dans ce genre de théorème ça permet de l'appliquer...
Et en l'occurrence ici, en fait je pense que 1 doit juste être intégrable, or pour que ça soit vrai il faut le restreindre à un intervalle, par exemple [0,1], intervalle qui n'a en vrai pas de rapport avec la fonction que l'on veut majorer...?