Intégration de Riemann
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 13:15
par barbu23 » 09 Jan 2015, 13:15
Bonjour à tous, :happy3:
J'aimerais que vous m'aidiez à calculer l'intégrale de Riemann suivante :
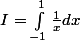
.
Voiçi comment je fais le calcul :
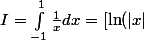 ]_{-1}^1 = 0)
Mais, je ne suis pas sûr de ce calcul s'il est juste ou non, car, il y'a une singularité :

de la fonction

. Je ne sais pas si ça a un impact sur le résultat qu'on obtient, ou bien ça n'a aucun effet.
Merci pour vos éclaircissements. :happy3:
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 09 Jan 2015, 13:45
par Monsieur23 » 09 Jan 2015, 13:45
Aloha,
Il me semble que le théorème fondamental de l'intégration n'est valable que les fonctions continues (par morceaux) sur un segment non ?
« Je ne suis pas un numéro, je suis un homme libre ! »
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 13:57
par barbu23 » 09 Jan 2015, 13:57
Monsieur23 a écrit:Aloha,
Il me semble que le théorème fondamental de l'intégration n'est valable que les fonctions continues (par morceaux) sur un segment non ?
Merci beaucoup pour cette réponse. :happy3:
Est ce que cela veut dire, qu'on ne peut pas calculer :
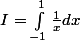
? Et qu'est ce que ça veut dire concrètement : fonction continue par morceaux ?

est - elle continue par morceaux ?
Merci d'avance. :happy3:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Jan 2015, 14:00
par arnaud32 » 09 Jan 2015, 14:00
barbu23 a écrit:Merci beaucoup pour cette réponse. :happy3:
Est ce que cela veut dire, qu'on ne peut pas calculer :
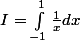
? Et qu'est ce que ça veut dire concrètement : fonction continue par morceaux ?

est - elle continue par morceaux ?
Merci d'avance. :happy3:
elle n'est meme pas define en 0
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Jan 2015, 15:11
par arnaud32 » 09 Jan 2015, 15:11
pour a, b positifs tels que

=\int_{-1}^{-a}\frac{dx}{x}+\int_{b}^{1}\frac{dx}{x}=ln(a/b))
tu vois bien que f n'a pas de limite en (0,0)
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 09 Jan 2015, 15:51
par SLA » 09 Jan 2015, 15:51
arnaud32 a écrit:pour a, b positifs tels que

=\int_{-1}^{-a}\frac{dx}{x}+\int_{b}^{1}\frac{dx}{x}=ln(a/b))
tu vois bien que f n'a pas de limite en (0,0)
Enfin, on voit quand même que si a=b, on a une limite. On en revient encore à la valeur principale de Cauchy...
Pablo, quand vas-tu commencer à regarder les définitions? La fonction 1/x n'est pas continue par morceau sur [-1,1] donc pas Riemann intégrable, ni même via une intégrale généralisée.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 09 Jan 2015, 16:00
par arnaud32 » 09 Jan 2015, 16:00
SLA a écrit:Enfin, on voit quand même que si a=b, on a une limite. On en revient encore à la valeur principale de Cauchy...
Pablo, quand vas-tu commencer à regarder les définitions? La fonction 1/x n'est pas continue par morceau sur [-1,1] donc pas Riemann intégrable, ni même via une intégrale généralisée.
en prenant
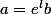
tu as meme le choix de la limite que tu veux, c'est d'ailleurs ce qui prouve qu'il n'y pas de limite pour (x,y) ->(0,0) (avec x et y independants)
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 09 Jan 2015, 18:17
par paquito » 09 Jan 2015, 18:17
Ca na aucun sens, la somme de 2 intégrales divergentes ne peut rien donner, quand bien même l'intégrante est impaire!
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 09 Jan 2015, 19:39
par SLA » 09 Jan 2015, 19:39
paquito a écrit:Ca na aucun sens, la somme de 2 intégrales divergentes ne peut rien donner, quand bien même l'intégrante est impaire!
Non et c'est bien pour ça qu'Arnaud introduit les paramètres a et b.
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Jan 2015, 09:03
par paquito » 10 Jan 2015, 09:03
Je répète que

n'a aucun sens; revoyez votre cours l faudrait que:
 et
et
soient convergentes.
Voir n'importe quel bouquin de prépa.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 10 Jan 2015, 09:14
par chan79 » 10 Jan 2015, 09:14
paquito a écrit:Je répète que

n'a aucun sens
Voir n'importe quel bouquin de prépa.
Bien-sûr, tout ce qu'on peut dire, c'est que:

-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 10 Jan 2015, 10:21
par SLA » 10 Jan 2015, 10:21
paquito a écrit:Je répète que

n'a aucun sens; revoyez votre cours l faudrait que:
 et
et
soient convergentes.
Voir n'importe quel bouquin de prépa.
La raison que tu donnes n'est même pas bonne. La fonction 1/x n'est pas continue par morceaux sur [-1,1], donc pas intégrable.
Ça aussi c'est dans les bouquins de prepa.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Jan 2015, 13:14
par barbu23 » 10 Jan 2015, 13:14
Merci à vous tous pour vos réponses.
Et si on considère que

est définie et continue en

tel que :
 = \infty \in \mathbb{P}^1 ( \mathbb{R} ))
et
)
? Est ce que dans ce cas là :

existe ? et elle vaut combien ?
Merci d'avance. :happy3:
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Jan 2015, 13:36
par paquito » 10 Jan 2015, 13:36
On pourrait avoir envie d'écrire \bigint\{-1}^{1}\frac{1}{x}dx=0, mais x->\frac{1}{x} ne sera jamais continue sur [-1; 1]et cette intégrale ne peut pas être considérée comme convergente en ???; il y a des définitions précises; quant à poser f(0)=oo ???
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Jan 2015, 13:38
par paquito » 10 Jan 2015, 13:38
SLA a écrit:La raison que tu donnes n'est même pas bonne. La fonction 1/x n'est pas continue par morceaux sur [-1,1], donc pas intégrable.
Ça aussi c'est dans les bouquins de prepa.
C'est une bonne raison supplémentaire!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Jan 2015, 13:49
par Doraki » 10 Jan 2015, 13:49
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Jan 2015, 13:56
par barbu23 » 10 Jan 2015, 13:56
paquito a écrit:On pourrait avoir envie d'écrire \bigint\{-1}^{1}\frac{1}{x}dx=0, mais x->\frac{1}{x} ne sera jamais continue sur [-1; 1]et cette intégrale ne peut pas être considérée comme convergente en ???; il y a des définitions précises; quant à poser f(0)=oo ???
 = \dfrac{1}{x})
est une homographie qui est une application continue
 \to \mathbb{P}^1 ( \mathbb{R} ))
tel que :
 = \infty)
et
 = 0)
. La topologie de
 = \mathbb{R} \bigcup \{ \infty \})
est la topologie définie par :
Les ouverts sont les ouverts de

+ Les ouverts

avec

est le complémentaire d'un compact

de

.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Jan 2015, 14:01
par barbu23 » 10 Jan 2015, 14:01
Je ne comprends pas de quoi tu parles. Tu me pointes du doigt l'erreur que je fais, sinon, je ne peux pas avancer. :happy3:
-
paquito
- Membre Complexe
- Messages: 2168
- Enregistré le: 26 Fév 2014, 12:55
-
 par paquito » 10 Jan 2015, 15:07
par paquito » 10 Jan 2015, 15:07
Le fait de se placer dans un compacifié de

n'arrange rien; qu'elle est l'image réciproque de l'ouvert

)
; de plus une fonction continue sur un compact K est uniformément continue sur K. Qu'est ce qu'il en est ici?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Jan 2015, 15:25
par barbu23 » 10 Jan 2015, 15:25
paquito a écrit:Le fait de se placer dans un compacifié de

n'arrange rien; qu'elle est l'image réciproque de l'ouvert

)
; de plus une fonction continue sur un compact K est uniformément continue sur K. Qu'est ce qu'il en est ici?
 = ] - 1 , 1 [)
???.
Par contre, je ne comprends pas ta deuxième question. Pourquoi évoques tu l'uniforme continuité ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
n'a aucun sens; revoyez votre cours l faudrait que:
et
soient convergentes.
n'arrange rien; qu'elle est l'image réciproque de l'ouvert

; de plus une fonction continue sur un compact K est uniformément continue sur K. Qu'est ce qu'il en est ici?