Bonsoir je bloque sur la question suivante depuis un bon bout de temps, j'ai l'impression de louper qque chose de pourtant évident ms rien à faire les heures passent et j'arrive pas...alors voilà:
f(x)=Int(t^(-x)*(1+t)^(1/2),x=0..1) définie sur ]-infinité,0[.
A l'aide d'une intégration par parties trouver une relation entre f(x) et f(x+1).
Voilà à vos stylo et brouillons, merci pr votre aide.
Intégration par parties
9 messages
- Page 1 sur 1
Salut et re,
L'ipp donne quand même quelquechose. En fait, faut remarquer qu'on parle de f(x) et non f(t).
Donc deja en remplacant x par x+1, on voit qu'on a t^ {-x-1} qui apparait.
Donc on peut deja penser que faudra dériver t^{-x} en faisant l'IPP.
Apres, ben c'est classique :
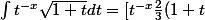^{ \frac{3}{2}}] - \frac{2}{3} \int (1+t) \sqrt{1+t}\frac{t^{-x-1}}{-x-1}=[blabla] + \frac{2}{3(x+1)} \int f(x+1)(1+t)\sqrt{1+t}dt)
Sauf boulette
Je m'y suis penché effectivement ^^
Ca ressemble à la fonction d'Euler... mais euh l'IPP ne donne pas grand chose il faut bien avouer ^^
L'ipp donne quand même quelquechose. En fait, faut remarquer qu'on parle de f(x) et non f(t).
Donc deja en remplacant x par x+1, on voit qu'on a t^ {-x-1} qui apparait.
Donc on peut deja penser que faudra dériver t^{-x} en faisant l'IPP.
Apres, ben c'est classique :
Sauf boulette
la vie est une fête 
fatal_error a écrit:Apres, ben c'est classique :
Sauf boulette
Salut! Désolé de répondre qu'aujourd'hui j'avais DS de maths ce matin (c'est tombé sur le centrale 98 aie aie). Deja merci d'y avoir jeté un coup d'oeil, c'est sympa
J'ai pas du donner clairement la fonction car tu as fais comme si:
dans ton calcul alors que la fonction f est définie ainsi:
J'ai réessayer ms toujours sans succès :mur:
PS: c'est tiré d'un centrale 95... :euh:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
