Intégration par parties ??
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Naths
- Membre Naturel
- Messages: 16
- Enregistré le: 07 Juil 2013, 16:36
-
 par Naths » 09 Juil 2013, 18:35
par Naths » 09 Juil 2013, 18:35
Bonsoir tlm :salut:
J'ai besoin d'aide pour déterminer la valeur de l'intégrale suivante :

-
Black Jack
 par Black Jack » 09 Juil 2013, 19:06
par Black Jack » 09 Juil 2013, 19:06
x².arctg(x)/(1+x²) = (x²+1-1).arctg(x)/(1+x²) = arctg(x) - arctg(x)/(1+x²)
S x².arctg(x)/(1+x²) dx = S arctg(x) dx - S arctg(x)/(1+x²) dx
a)
S arctg(x) dx
Poser arctg(x) = u ---> dx/(x²+1) = du
et poser dx = dv ---> x = v
S arctg(x) dx= x.artg(x) - S x/(x²+1) dx
S arctg(x) dx= x.artg(x) - (1/2).ln(x²+1)
b)
S arctg(x)/(1+x²) dx = (1/2) arctg²(x)
Et donc : S x².arctg(x)/(1+x²) dx = x.artg(x) - (1/2).ln(x²+1) - (1/2) arctg²(x)
Reste à calculer l'intégrale (en connaissant une primitive) en tenant compte des bornes d'intégration.
...
:zen:
-
Naths
- Membre Naturel
- Messages: 16
- Enregistré le: 07 Juil 2013, 16:36
-
 par Naths » 09 Juil 2013, 19:26
par Naths » 09 Juil 2013, 19:26
Merci !! :+++:
mais franchement je n'arrive pas à comprendre comment :
(x^2 * arctan(x) + arctan(x)) / 1+x^2 = arctan(x) "la première ligne"
-
Naths
- Membre Naturel
- Messages: 16
- Enregistré le: 07 Juil 2013, 16:36
-
 par Naths » 09 Juil 2013, 19:28
par Naths » 09 Juil 2013, 19:28
Naths a écrit:Merci !! :+++:
mais franchement je n'arrive pas à comprendre comment :
(x^2 * arctan(x) + arctan(x)) / 1+x^2 = arctan(x) "la première ligne"
c'est bon lol quel idiot :lol5: merci bcp ^^
-
LA solution
- Membre Relatif
- Messages: 165
- Enregistré le: 28 Déc 2012, 17:11
-
 par LA solution » 10 Juil 2013, 21:47
par LA solution » 10 Juil 2013, 21:47
salut
as tu utilise ca: arctanx/x carre+1 comme primitive de moins(1/2)arctanx
-
Black Jack
 par Black Jack » 11 Juil 2013, 06:32
par Black Jack » 11 Juil 2013, 06:32
LA solution a écrit:salut
as tu utilise ca: arctanx/x carre+1 comme primitive de moins(1/2)arctanx
Ce n'est pas exact, c'est plutôt :
F(x) = (1/2).(arctan(x))
² est une primitive de f(x) = arctan(x)/
(x²+1
) :zen:
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 11 Juil 2013, 06:46
par deltab » 11 Juil 2013, 06:46
Bonjour.
}{x^2+1}dx)
est de la forme
u'(x)dx)
-
Aredhell
- Membre Naturel
- Messages: 40
- Enregistré le: 02 Juin 2013, 19:35
-
 par Aredhell » 11 Juil 2013, 10:18
par Aredhell » 11 Juil 2013, 10:18
LA solution a écrit:salut
as tu utilise ca: arctanx/x carre+1 comme primitive de moins(1/2)arctanx
On a
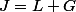
où

et
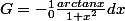
d'où:
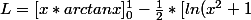]_{0}^{1})
et :
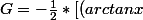^2]_{0}^{1})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités

