Intégration par changement de variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 29 Mai 2007, 10:53
par le fouineur » 29 Mai 2007, 10:53
Bonjour à tous,
J'ai du mal à appliquer le changement de variable à l'intégrale suivante:

Si je fais le changement de variable proposé: x=1/t j'ai
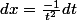
cette forme n'apparait pas dans l'intégrale proposée....Comment faire?
merci de me répondre
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 29 Mai 2007, 11:14
par anima » 29 Mai 2007, 11:14
le fouineur a écrit:Bonjour à tous,
J'ai du mal à appliquer le changement de variable à l'intégrale suivante:

Si je fais le changement de variable proposé: x=1/t j'ai
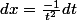
cette forme n'apparait pas dans l'intégrale proposée....Comment faire?
merci de me répondre
J'ai peut-etre fait une erreur, mais ca marche plutot bien ce changement de variable...
t=1/x
dx=-1/t^2 dt

Apres... a toi de voir. Mais ca simplifie grandement, c'estl e cas de le dire.
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 29 Mai 2007, 13:02
par le fouineur » 29 Mai 2007, 13:02
Bonjour anima et merci pour ta réponse rapide,
Je n'ai guère progressé depuis ton intervention,je suis arrivé à:

Et je ne vois pas comment faire apparaitre une forme en:
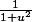
,Pourrais-tu me donner de nouvelles indications pour continuer?
D'avance merci
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 29 Mai 2007, 13:09
par mehdi-128 » 29 Mai 2007, 13:09
Bonjour la primitive de 1/sqrt(1-x^2) est arcsin(x).
Or, -dt/sqrt(1-2t^2)=-dt/sqrt(1-(sqrt(2)t)^2)
Ainsi ton intégrale vaut: -arcsin(sqrt(2)*t)
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 29 Mai 2007, 13:28
par le fouineur » 29 Mai 2007, 13:28
Bonjour medhi- 128 et merci pour ta réponse,
Tu as oublié le 1/2 sous la racine il me semble....
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 29 Mai 2007, 13:32
par anima » 29 Mai 2007, 13:32
le fouineur a écrit:Bonjour medhi- 128 et merci pour ta réponse,
Tu as oublié le 1/2 sous la racine il me semble....
Il n'a pas fait comme toi.
^2})
On obtient donc
 = -\frac{1}{\sqrt{1-(\sqrt{2} t)^2}})
=-Arcsin(\sqrt{2}t)+k)
D'ou
=-Arcsin(\frac{\sqrt{2}}{x})+k)
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 29 Mai 2007, 13:44
par le fouineur » 29 Mai 2007, 13:44
Merci anima pour ta réponse,
Pourrais-tu revenir au message #3, d'après Mathematica la forme finale à obtenir est en arctan... La transformation que j'ai effectuée est t'elle correcte? Si oui comment continuer le calcul?
Merci de me répondre
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 29 Mai 2007, 18:04
par Pythales » 29 Mai 2007, 18:04
J'ai l'impression qu'il est plus simple de poser
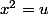
puis
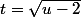
et ça donne bien un arctg
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 03 Juin 2007, 17:00
par le fouineur » 03 Juin 2007, 17:00
Bonjour à tous et merci Pythales pour ta réponse,
Il semble que le changement de variable proposé dans l'énoncé, soit x=1/t soit erroné.....En choisissant comme changement de variable

, on arrive après simplifications à:
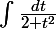
Comment faut-t'il procéder pour faire apparaitre une forme du type:
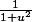
?
Merci de me répondre
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 03 Juin 2007, 17:09
par anima » 03 Juin 2007, 17:09
le fouineur a écrit:Bonjour à tous et merci Pythales pour ta réponse,
Il semble que le changement de variable proposé dans l'énoncé, soit x=1/t soit erroné.....En choisissant comme changement de variable

, on arrive après simplifications à:
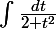
Comment faut-t'il procéder pour faire apparaitre une forme du type:
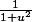
?
Merci de me répondre
} \\<br />= \frac{1}{2} \int \frac{dt}{1 + (\frac{t}{\sqrt{2})^2})
u =
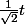
du =
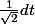
Donc dt =

du.
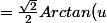 + k \\<br />= \frac{\sqrt{2}}{2} Arctan(\frac{t}{\sqrt{2}})+k)
-
le fouineur
- Membre Relatif
- Messages: 145
- Enregistré le: 01 Mai 2006, 10:21
-
 par le fouineur » 03 Juin 2007, 17:23
par le fouineur » 03 Juin 2007, 17:23
Merci anima pour ta réponse rapide
Ce problème est enfin terminé....
Cordialement le fouineur
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
, on arrive après simplifications à:
?