Intégration de fraction rationnelle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Altarov
- Messages: 3
- Enregistré le: 15 Avr 2017, 18:34
-
 par Altarov » 20 Avr 2017, 11:38
par Altarov » 20 Avr 2017, 11:38
Bonjour !
Je bloque complètement sur une primitive de fraction rationnelle :

J'ai décomposé la fraction comme ceci grâce à une division euclidienne :

Et vu que je suis très mauvais en intégration, je ne parviens pas à trouver la primitive de la partie de droite...
Je connais le résultat grâce à la machine, mais j'aimerai pouvoir le refaire plus tard..
Merci à vous !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 20 Avr 2017, 11:50
par Ben314 » 20 Avr 2017, 11:50
Salut,
Clairement, une première fonction dont la dérivée est de la forme

c'est
)
.
Et, comme
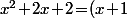^2\!+\!1)
une autre fonction qui a une dérivée de cette forme est
)
.
En prenant une combinaison linéaire bien choisie des deux, tu trouve une primitive de

P.S. : ta division euclidienne est clairement fausse.
Modifié en dernier par
Ben314 le 20 Avr 2017, 11:52, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Altarov
- Messages: 3
- Enregistré le: 15 Avr 2017, 18:34
-
 par Altarov » 20 Avr 2017, 12:03
par Altarov » 20 Avr 2017, 12:03
Merci pour ta réponse !
Comme je te le disais, je suis très mauvais en intégration, je pensais que ln(u) ne s'appliquait que pour u'/u, or, ici, on ne peut pas faire apparaître u' en haut ?
La factorisation du dénominateur est quelque chose qui ne me serait pas venu à l'esprit, voilà pourquoi je n'apprécie pas cette partie des mathématiques

Effectivement je m'était trompé sur la division euclidienne, merci !
-
Altarov
- Messages: 3
- Enregistré le: 15 Avr 2017, 18:34
-
 par Altarov » 20 Avr 2017, 12:18
par Altarov » 20 Avr 2017, 12:18
J'ai trouvé finalement !
Il fallait juste décomposer cette partie en :
^2+1})
Ce qui nous donne :
F(x) =
 + 2*\tan^{-1} (x+1))
Merci infiniment !
Bonne journée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités

