Tuvasbien a écrit:Bonjour, étudie
=\left(\int_0^x{f(t)dt}\right)e^{-kx})
Bonjour et merci beaucoup pour cette idée géniale qui mène à une résolution courte et élégante !
Je n'y aurais jamais pensé, d'autant que je persistais à vouloir appliquer les accroissements finis à l'intégrale et que les demi souvenirs que j'avais ne concernent visiblement pas cet exercice.
Cela dit, ça m'a fait penser à une des pistes que j'avais essayé d'explorer et qui passait par la dérivée logarithmique mais je n'arrive pas à conclure et je ne sais pas si c'est possible.
On montre facilement que, si f n'est pas identiquement nulle, donc qu'il existe un

tel que
\neq 0)
on peut définir la fonction

par
 = \int_{0}^{x}{f(t) dt})
et
 = ln (F(x)))
On a donc
>0)
pour
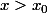
L'inégalité de départ
 \leq k F(x))
donne donc, pour x \geq x_0
}{F(x)} \leq k)
d'où
 \leq k)
On peut donc en déduire (je tenais à mes accroissements finis)
 - \varphi (x_0) \leq k (x-x_0))
plus, en ne gardant que
)
et en prenant l'exponentielle de chaque membre, on en déduisait que
 \leq k K e^{kx})
(avec K une constante obtenue en réunissant tous les autres termes).
J'en était resté là… avais-je une chance de retomber sur ton idée géniale ?
Parce que, ce que je me demande aussi, c'est comment on fait pour y penser, et que je ne sais pas si je m'étais complètement égaré ou si j'était sur une bonne piste (à cause des exponentielles)…
