Intégration difficile
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
michastro
- Messages: 2
- Enregistré le: 03 Mar 2016, 15:21
-
 par michastro » 17 Fév 2022, 17:16
par michastro » 17 Fév 2022, 17:16
Bonjour,
Je suis sur un exercice de calcul de déviation d'un rayon lumineux en mécanique newtonienne, j'arrive sur ça:

Je n'arrive pas ou je ne sais plus comment résoudre ça.
Merci de vos avis
Michel
-
mathelot
 par mathelot » 17 Fév 2022, 17:39
par mathelot » 17 Fév 2022, 17:39
Bonjour,
On factorise par R au dénominateur, on pose le changement de variable
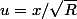
puis l'intégrale se primitive, en effet
^{\frac{3}{2}}} dx = \dfrac {x}{\sqrt{x^2+1}})
L'intégrale vaut

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 17 Fév 2022, 17:50
par Pisigma » 17 Fév 2022, 17:50
Bonjour,
ça marche aussi en posant
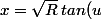)
avec
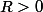
-
michastro
- Messages: 2
- Enregistré le: 03 Mar 2016, 15:21
-
 par michastro » 17 Fév 2022, 18:07
par michastro » 17 Fév 2022, 18:07
Merci beaucoup,
Ce qui me fait pour mon intégrale (en prenant abs(x) pour avoir mon accélération toujours dans le bon sens) une valeur de 2!! Exactement ce que j'attendais mais que je ne trouvais pas.
-
Black Jack
 par Black Jack » 17 Fév 2022, 18:42
par Black Jack » 17 Fév 2022, 18:42
Bonjour,
Poser x = V(R) * tan(t) (avec V pour racine carrée)
R + x² = R*(1 + tan²(t)) = R/cos²(t)
dx = V(R) * dt/cos²(t)
dx/(R + x²)^(3/2) = V(R) * dt/cos²(t) * cos³(t)/R^(3/2)
dx/(R + x²)^(3/2) = (1/R) * cos(t) dt
x = -oo --> t = -Pi/2
x = +oo --> t = Pi/2
Donc
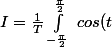.dt)
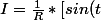]_{-\frac{\pi}{2}}^{\frac{\pi}{2}})


Edit : Pas vu le message de Pisigma.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités

