[MPSI] intégration et changement de variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 22 Fév 2007, 11:57
par pouik » 22 Fév 2007, 11:57
Bonjour,
Je souhaiterait calculer une primitive de ces deux fonctions :
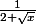
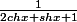 mais je ne vois pas les changements de variable adéquat.
mais je ne vois pas les changements de variable adéquat.Merci d'avnace pour votre aide.
-
mathelot
 par mathelot » 22 Fév 2007, 12:13
par mathelot » 22 Fév 2007, 12:13
Bonjour,
pour la première,
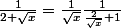
et
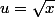
d'où:
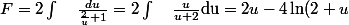 = 2\sqrt{x} - 4 \ln ( 2 + \sqrt{x}))
pour la seconde:
on revient à la déf:
=\frac{e^{x}+e^{-x}}{2})
=\frac{e^{x}-e^{-x}}{2})
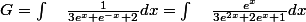
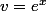
et on obtient une fraction rationnelle en v.
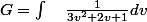
qui s'intègre en arctangente car

est strictemnt négatif.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 22 Fév 2007, 16:49
par pouik » 22 Fév 2007, 16:49
J'ai essayé de faire le 1. en passant par votre changement de variable mais je suis bloqué. Pourriez vous m'aider à me débloquer. Merci d'avance.
Soit

la fonction définie sur
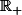
par :
 = \displaystyle\int_{0}^{x} f(t) dt)

est une primitive de

sur
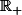
.
Soient
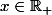
.
Calculons
)
en utilisant la
Formule de changement de variable.
Soit
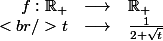
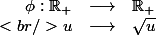

étant de classe
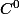
sur
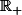
.

est de classe

sur
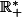
, à valeurs dans
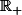
.
et :
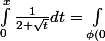}^{\phi(x^2)} f(t) dt)
d'où, d'après la
Formule de changement de variable :
 = \displaystyle\int_{0}^{x^2} f(\phi(u)) \phi'(u) du)
c'est-à-dire :
 = \displaystyle\int_{0}^{x^2} \frac{1}{2+u} \times \frac{1}{2\sqrt{u}} du)
c'est-à-dire :
 = \displaystyle\int_{0}^{x^2} \frac{1}{(2+u) 2\sqrt{u}} du)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Fév 2007, 17:22
par Nightmare » 22 Fév 2007, 17:22
Bonjour
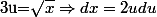
on en déduit :

qui se calcul facilement.
:happy3:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 22 Fév 2007, 18:05
par pouik » 22 Fév 2007, 18:05
Faut-il faire une intégration par parties ??
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Fév 2007, 18:11
par Nightmare » 22 Fév 2007, 18:11
Non
Remarque juste que 2u=2(u+2)-4
:happy3:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 22 Fév 2007, 18:26
par pouik » 22 Fév 2007, 18:26
c'est-à-dire (puisque
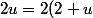 - 4)
) :
 = \displaystyle\int_{0}^{x^2} \frac{2(2+u) - 4}{2+u} du)
c'est-à-dire :
 = \displaystyle\int_{0}^{x^2} 2 - 4\frac{1}{2+u} du)
c'est-à-dire :
 = \left[2u - 4\ln{(2+u)}\right]_{0}^{x^2})
c'est-à-dire :
 = \left(2x^2 - 4\ln{(2+x^2)}\right) - \left(2 \times 0 - 4\ln{(2+0)}\right))
c'est-à-dire :
 = 2x^2 - 4\ln{\left(\frac{2+x^2}{2}\right)})
Est-ce correct ??
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 22 Fév 2007, 19:01
par Nightmare » 22 Fév 2007, 19:01
C'est ça :happy3:
-
mathelot
 par mathelot » 22 Fév 2007, 19:41
par mathelot » 22 Fév 2007, 19:41
je crois pas car
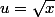
. le résultat est plus simple.
c'est celui que j'ai donné à 12h13.
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 22 Fév 2007, 19:55
par pouik » 22 Fév 2007, 19:55
le problème vient peut-être an fait du choix de

: il faudrait peut-etre prendre
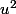
, comme ca on aura les

NON ?? Sinon d'où vient l'erreur ??
-
mathelot
 par mathelot » 22 Fév 2007, 21:42
par mathelot » 22 Fév 2007, 21:42
Nightmare a écrit:Bonjour
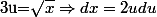
on en déduit :

qui se calcul facilement.
:happy3:
pouïk,
je reprend l'explication de Nightmare.
on pose
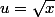
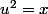
en différentiant:
2udu=dx
et tu remplaces dx en fonction de u et du. :marteau:
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 23 Fév 2007, 10:20
par pouik » 23 Fév 2007, 10:20
Bonjour,
MAis donc il faut plutot poser :
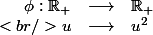
NON ?? (avec mon raisonnement)
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Fév 2007, 11:08
par pouik » 26 Fév 2007, 11:08
Bonjour,
Pour la deuxième, je propose (il y avait une erreur dans ce qu'on me proposait : 2 au numérateur en fait), et sinon pour calculer l'intégrale en arctangente, je me suis servi de la calculatrice donc si vous pouviez m'expliquer comment le faire à la main, ce serait vraiment formidable. Merci d'avance :
Posons
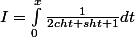
.
Travail préliminaire : Soit
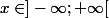
.
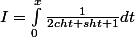
c'est-à-dire :
 + \left(\frac{e^t - e^{-t}}{2}\right) + 1} dt)
c'est-à-dire, après
simplification :
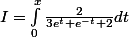
c'est-à-dire :
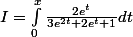
c'est-à-dire :
^2 + 2e^{t} + 1} \times e^t dt)
Soit

et

définies par :
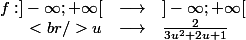
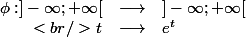

étant de classe
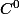
sur
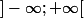
.

est de classe

sur
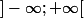
, à valeurs dans

.
Comme :
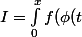)\phi'(t) dt)
Selon la
Formule du Changement de Variable :
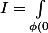}^{\phi(x)} f(u) du)
c'est-à-dire :
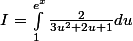
c'est-à-dire :
}{2}\right)}\right]_1^{e^x})
c'est-à-dire :
}{2}\right)}\right]_1^{e^x})
c'est-à-dire :
}{2}\right)}\right) - \left(\sqrt{2}\arctan{\left(\frac{\sqrt{2}(3+1)}{2}\right)}\right))
c'est-à-dire :
}{2}\right)}\right) - \left(\sqrt{2}\arctan{\left(\sqrt{2}2!\right)}\right))
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Fév 2007, 11:13
par fahr451 » 26 Fév 2007, 11:13
bonjour
je ne comprends pas la question
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Fév 2007, 11:36
par pouik » 26 Fév 2007, 11:36
En fait je calcule la deuxième intégrale donnée dans mon premier message. Et je souhaiterait saoir si c'est bon.
De plus, je ne sais paas calculer à la main une primitive de
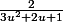
, je l'ai fait ici à la calculette : pourriez vous m'expliquer comment le faire à la main.
Merci d'avance. :zen: :zen:
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Fév 2007, 12:03
par fahr451 » 26 Fév 2007, 12:03
mettre sous forme canonique
3u^2 +2u+1 = 3 [ (u+1/3)^2 + 2/9 ] = (2/3)[ (u+1/3)(3/racine(2) )^2 +1 ]
poser
v = (3/racine(2) (u+1/3) et reconnaitre la dérivée d ' arctan v
-
pouik
- Membre Rationnel
- Messages: 516
- Enregistré le: 12 Oct 2006, 16:16
-
 par pouik » 26 Fév 2007, 12:30
par pouik » 26 Fév 2007, 12:30
Est-ce que ce que j'ai écrit est bon.
SInon comment faites vous pour faire apparaitre cette égalité : y a t il un "truc" ?
fahr451 a écrit:mettre sous forme canonique
3 [ (u+1/3)^2 + 2/9 ] = (2/3)[ (u+1/3)(3/racine(2) )^2 +1 ]
-
Edrukel
- Membre Relatif
- Messages: 132
- Enregistré le: 17 Déc 2006, 10:07
-
 par Edrukel » 01 Mar 2007, 12:31
par Edrukel » 01 Mar 2007, 12:31
on montre que 1/(2chx+shx+1)=(2e^x)/(3e^(2x)+2e^x+1)
on faisant le changement de variable
prenons la fonction phi:]1,+oo[-->IR
phi(x)=ln((x-1)/3) , phi est bien à valeurs de IR qui l'ensemble de départ de f
alors pour tout x de IR, on a Int( f(t)dt,t=0..x)=Int(f(t)dt,t=phi(4)..phi(3e^x+1)) ,comme 3e^x+1 et 4 sont dans ]1,+oo[
d'où d'après FCV :
Int(f(t)dt,t=0..x)=Int((2/(2+t^2)]dt,t=4..(3e^x+1))=rac(2)arctan((3e^x+1)/rac(2))-rac(arctan(2*rac(2)))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités