Intégration et changement de variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jacky22
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Sep 2012, 11:03
-
 par Jacky22 » 14 Jan 2014, 11:22
par Jacky22 » 14 Jan 2014, 11:22
Bonjour,
Je cherche à intégrer
^2}{g(x)})}dx)
Voici ce que je propose :
Je pose
=\sqrt{\frac{f'(x)^2}{g(x)}})
.
Ensuite, je fait le changement de variable
=cos(y))
.
Mais du coup j'arrive à
dx=-sin(y)dy)
Comme je n'ai pas "dx=..." mais "h'(x)dx=...", j'ai l'impression que ce n'est pas la bonne méthode.
Est-ce que quelqu'un pourrait m'aiguiller?
Merci par avance.
-
Jacky22
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Sep 2012, 11:03
-
 par Jacky22 » 14 Jan 2014, 12:08
par Jacky22 » 14 Jan 2014, 12:08
Je me suis dit qu'une intégration par partie pourrait être utile si je fais u=
)^2})
et v'=1 dès le départ.
Ensuite, je fais le même changement de variable.
J'ai l'impression que je peux la résoudre.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 17 Jan 2014, 12:01
par deltab » 17 Jan 2014, 12:01
Bonjour
Jacky22 a écrit:Je me suis dit qu'une intégration par partie pourrait être utile si je fais u=
)^2})
et v'=1 dès le départ.
Ensuite, je fais le même changement de variable.
J'ai l'impression que je peux la résoudre.
Je ne le crois pas sans d'autres conditions. La fonction à intégrer est-elle définie sur ]a,b[ exemple
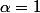
,

,
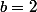
,
=x)
et
=\dfrac{1}{x})
.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 17 Jan 2014, 12:05
par deltab » 17 Jan 2014, 12:05
Bonjour
Jacky22 a écrit:Je me suis dit qu'une intégration par partie pourrait être utile si je fais u=
)^2})
et v'=1 dès le départ.
Ensuite, je fais le même changement de variable.
J'ai l'impression que je peux la résoudre.
Je ne le crois pas sans d'autres conditions. La fonction à intégrer est-elle définie sur ]a,b[ exemple
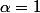
,

,
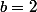
,
=x)
et
=\dfrac{1}{x})
(ou
=\dfrac{1}{x^n},)
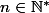)
.
-
Jacky22
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Sep 2012, 11:03
-
 par Jacky22 » 17 Jan 2014, 14:17
par Jacky22 » 17 Jan 2014, 14:17
Oui, effectivement, mes hypothèses de départs sont simples : f et g sont des fonctions suffisamment régulières pour être intégrables et dérivables sur l'espace d'intégration. Pas de problème de ce côté là, h est intégrable.
Il faut également encadrer
|<=1/\sqrt(\alpha))
. Avec tout ça, j'arrive alors au résultat suivant :
^2}dx=[(x-1)\sqrt{1-\alpha h(x)^2}]_{\Omega})
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 18 Jan 2014, 10:04
par deltab » 18 Jan 2014, 10:04
Bonjour
Jacky22 a écrit:Oui, effectivement, mes hypothèses de départs sont simples : f et g sont des fonctions suffisamment régulières pour être intégrables et dérivables sur l'espace d'intégration. Pas de problème de ce côté là, h est intégrable.
Il faut également encadrer
|<=1/\sqrt(\alpha))
. Avec tout ça, j'arrive alors au résultat suivant :
^2}dx=[(x-1)\sqrt{1-\alpha h(x)^2}]_{\Omega})
Déjà, il faut que l'ensemble
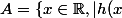|\le \dfrac{1}{\sqrt{\alpha}}\rbrace)
soit non vide et les bornes d'intégration ne peuvent être alors prises que dans le même intervalle contenu dans A.
Comment as-tu trouvé que
^2}dx=[(x-1)\sqrt{1-\alpha h(x)^2}]_{\Omega})

\sqrt{1-\alpha h(x)^2})
n'est pas une primitive de
^2})
-
Jacky22
- Membre Naturel
- Messages: 31
- Enregistré le: 22 Sep 2012, 11:03
-
 par Jacky22 » 18 Jan 2014, 10:58
par Jacky22 » 18 Jan 2014, 10:58
deltab a écrit:Bonjour
Déjà, il faut que l'ensemble
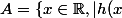|\le \dfrac{1}{\sqrt{\alpha}}\rbrace)
soit non vide et les bornes d'intégration ne peuvent être alors prises que dans le même intervalle contenu dans A.
Comment as-tu trouvé que
^2}dx=[(x-1)\sqrt{1-\alpha h(x)^2}]_{\Omega})

\sqrt{1-\alpha h(x)^2})
n'est pas une primitive de
^2})
Merci, A est non vide et les bornes sont bien-sûr dans A.
J'ai procédé de la manière suivante :
1) IPP :
^2}dx=[x\sqrt{1-\alpha h(x)^2}]_{\Omega}-\int_{\Omega}\frac{\frac{1}{2}(-2\alpha h'(x)h(x))}{\sqrt{1-\alpha h(x)^2}}dx)
2) Changement de variables
=cos(y))
:
dx=-sin(y)dy)
h(x))}{\sqrt{1-\alpha h(x)^2}}dx=\int_{arccos(\sqrt{\alpha}h(\Omega))}cos(y)sin(y)/|sin(y)|dy)
sin(y) est positive car
))
est compris entre 0 et pi.
Donc :
h(x))}{\sqrt{1-\alpha h(x)^2}}dx=\int_{arccos(\sqrt{\alpha}h(\Omega))}cos(y)dy=[\sqrt{1-\alpha h(x)^2}]_{\Omega})
car
)=\sqrt{1-x^2})
Merci de me dire si vous trouvez une erreur.
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 18 Jan 2014, 14:40
par deltab » 18 Jan 2014, 14:40
Bonjour
^2}dx=[x\sqrt{1-\alpha h(x)^2}]_{\Omega}-\int_{\Omega}\frac{\frac{1}{2}(-2\alpha h'(x)h(x))}{\sqrt{1-\alpha h(x)^2}}dx)
Il manque le facteur
x dans la 2ème intégrale.
^2}dx=[x\sqrt{1-\alpha h(x)^2}]_{\Omega}-\int_{\Omega})

h(x))}{\sqrt{1-\alpha h(x)^2}}dx)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
